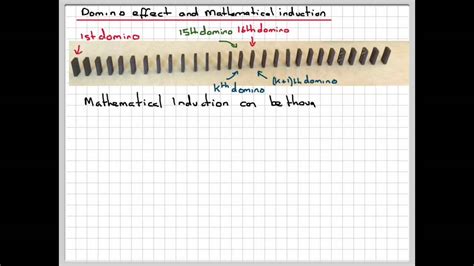
Induksi matematika adalah suatu teknik untuk membuktikan bahwa sebuah proposisi matematis berlaku untuk semua nilai, termasuk nilai yang tidak dikenal. Teknik ini dinamakan induksi karena kita memulai dari satu kasus (n=1) dan kemudian meningkatkan nilai-nila tersebut hingga kita mencapai hasil yang diinginkan.
Contoh 1: Bilangan Trianguler
Bilangan trianguler adalah bilangan yang dapat membentuk pola segi tiga. Misalnya, untuk n=3, kita memiliki pola segi tiga seperti berikut:
Prove that the n-th triangular number is:
Tn = n(n+1)/2
Step 1: Show it's true for n=1
T1 = 1 × (1+1) / 2 = 1 adalah benar.
Step 2: Assume it's true for n=k
Tk = k(k+1)/2 adalah benar (asumsi).
Step 3: Prove it's true for "k+1"
Tk+1 = (k+1)(k+2)/2 ?
We know that Tk = k(k+1)/2 (the assumption above), so we can do a replacement for all but the last term:
Tk+1 = Tk + (k + 1)
(k+1)(k+2)/2 = k(k+1) / 2 + (k+1)
Multiply all terms by 2:
(k + 1)(k + 2) = k(k + 1) + 2(k + 1)
(k + 1)(k + 2) = (k + 2)(k + 1)
They are the same! So it is true.
So: Tk+1 = (k+1)(k+2)/2 adalah benar.
Contoh 2: Penjumlahan Kube
Prove that:
13 + 23 + 33 + … + n3 = ¼n2(n + 1)2
Step 1: Show it's true for n=1
13 = ¼ × 12 × 22 adalah benar.
Step 2: Assume it's true for n=k
13 + 23 + 33 + … + k3 = ¼k2(k + 1)2 adalah benar (asumsi).
Step 3: Prove it's true for "k+1"
13 + 23 + 33 + … + (k + 1)3 = ¼(k + 1)2(k + 2)2 ?
We know that 13 + 23 + 33 + … + k3 = ¼k2(k + 1)2 (the assumption above), so we can do a replacement for all but the last term:
¼k2(k + 1)2 + (k + 1)3 = ¼(k + 1)2(k + 2)2
Multiply all terms by 4:
k2(k + 1)2 + 4(k + 1)3 = (k + 1)2(k + 2)2
All terms have a common factor (k + 1)2, so it can be canceled:
k2 + 4k + 4 = k2 + 4k + 4
They are the same! So it is true.
So: 13 + 23 + 33 + … + (k + 1)3 = ¼(k + 1)2(k + 2)2 adalah benar.
Your Turn
Coba Anda praktikkan sendiri pada dua contoh berikut:
Contoh 1: Bilangan Trianguler
Prove that the n-th triangular number is:
Tn = n(n+1)/2
Contoh 2: Penjumlahan Kube
Prove that:
13 + 23 + 33 + … + n3 = ¼n2(n + 1)2