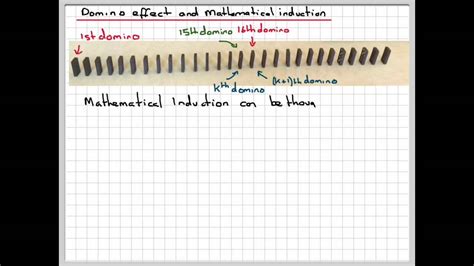
Dalam matematika, terkadang kita perlu membuktikan bahwa sebuah formula adalah benar. Dalam artikel ini, saya akan membahas bagaimana cara membuktikan bahwa formula K2 + (2(K+1)-1) = (K+1)^2 adalah benar.

Formula tersebut tampak seperti:

K2 + (2(k+1)-1) = (k+1)^2

Sekarang, mari kita expand semua term dan sederhanakan:

K2 + 2K + 2 – 1 = K2 + 2K + 1
Dan karena K2 + 2K + 1 = K2 + 2K + 1, maka formula tersebut benar.

Dengan demikian, kita telah membuktikan bahwa K2 + (2(K+1)-1) = (K+1)^2 adalah benar.

Sekarang, mari kita coba dua contoh lainnya untuk Anda praktekkan:

Contoh 1: Bilangan Triangular

Bilangan triangular adalah bilangan yang dapat dibentuk menjadi poligon segi tiga. Prove bahwa bilangan triangular ke-n adalah:

Tn = n(n+1)/2

1. Tunjukkan bahwa Tn adalah benar untuk n=1:
   T1 = 1 × (1+1) / 2 = 1, yang benar.

2. Asumsikan bahwa Tn adalah benar untuk n=k:
   Tk = k(k+1)/2, yang benar.
   Sekarang, mari kita buktikan bahwa Tk+1 juga benar:
   Tk+1 = (k+1)(k+2)/2, ?

Kita tahu bahwa Tk = k(k+1)/2, yang asumsi di atas.
Tk+1 memiliki baris tambahan (k + 1) titik.
Jadi, Tk+1 = Tk + (k + 1)
(k+1)(k+2)/2 = k(k+1) / 2 + (k+1)

Kita kalian semua term dengan 2:
(k + 1)(k + 2) = k(k + 1) + 2(k + 1)
(k + 1)(k + 2) = (k + 2)(k + 1)

Mereka adalah yang sama! Jadi, formula tersebut benar.
Jadi:
Tk+1 = (k+1)(k+2)/2 adalah benar.

Contoh 2: Penjumlahan Bilangan Kubik

Bilangan kubik adalah kuadrat bilangan alami. Prove bahwa:

13 + 23 + 33 + … + n3 = ¼n2(n + 1)2

1. Tunjukkan bahwa formula tersebut benar untuk n=1:
   13 = ¼ × 12 × 22, yang benar.

2. Asumsikan bahwa formula tersebut benar untuk n=k:
   13 + 23 + 33 + … + k3 = ¼k2(k + 1)2, yang benar.
   Sekarang, mari kita buktikan bahwa formula tersebut juga benar untuk "n+1":
   13 + 23 + 33 + … + (k + 1)3 = ¼(k + 1)2(k + 2)2, ?

Kita tahu bahwa 13 + 23 + 33 + … + k3 = ¼k2(k + 1)2, yang asumsi di atas.
Kita dapat melakukan penggantian untuk semua term kecuali yang terakhir:
¼k2(k + 1)2 + (k + 1)3 = ¼(k + 1)2(k + 2)2

Kita kalian semua term dengan 4:
k2(k + 1)2 + 4(k + 1)3 = (k + 1)2(k + 2)2
Semua term memiliki faktor umum yang sama, yaitu (k + 1)2, sehingga dapat dibatalkan:
k2 + 4(k + 1) = (k + 2)2

Dan sederhanakan:
k2 + 4k + 4 = k2 + 4k + 4
Mereka adalah yang sama! Jadi, formula tersebut benar.
Jadi:
13 + 23 + 33 + … + (k + 1)3 = ¼(k + 1)2(k + 2)2 adalah benar.

Dengan demikian, kita telah membuktikan bahwa K2 + (2(K+1)-1) = (K+1)^2 dan dua contoh lainnya adalah benar.