Dalam analisis data, kita seringkali dihadapkan pada situasi di mana kita memiliki sejumlah data yang terkait dan ingin menemukan pola atau hubungan antara dua variabel. Salah satu teknik statistik yang paling umum digunakan adalah membuat grafik scatter plot dan menentukan garis fitur terbaik (best fit line) untuk menjelaskan perilaku data.

Garis Fitur Terbaik

Garis fitur terbaik, juga disebut sebagai "Trend Line", adalah garis yang ditentukan dengan cara mencari nilai yang sepanjang mungkin dekat semua titik data, serta sebanyak mungkin titik di atas garis sebagai titik di bawah. Namun, untuk meningkatkan akurasi, kita dapat menggunakan metode Least Squares Regression dan Calculator Least Squares.

Contoh: Kenaikan Muka Air Laut

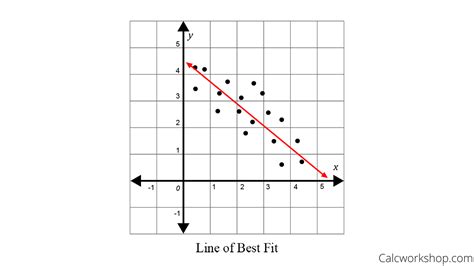
Berikut adalah contoh scatter plot kenaikan muka air laut:

Garis fitur terbaik yang saya gambar pada grafik di atas.
Interpolation dan Extrapolation

Interpolation adalah teknik untuk menemukan nilai di dalam set data. Dalam contoh di atas, kita menggunakan interpolation linear untuk menestimasi penjualan di 21°C.

Extrapolation adalah teknik untuk menemukan nilai di luar set data. Dalam contoh di atas, kita menggunakan extrapolation linear untuk menestimasi penjualan di 29°C (yang lebih tinggi daripada nilai yang ada). Namun, perlu diingat bahwa extrapolation dapat menghasilkan hasil yang tidak akurat karena kita berada di "wilayah tak diketahui".

Selain menggunakan grafik, kita juga dapat membuat formula untuk membantu kita.

Contoh: Persamaan Garis Sembilan

Kita dapat menestimasi persamaan garis lurus dari dua titik data pada grafik di atas. Mari kita asumsikan dua titik di sekitar nilai aktual: (12°, $180) dan (25°, $610). Pertama, temukan slope:

Slope "m" = perubahan y / perubahan x
= $610 – $180 / 25° – 12°
= $430 / 13°
≈ 33

Sekarang, masukkan slope dan titik (12°, $180) ke dalam formula "point-slope":
y – y1 = m(x – x1)
y – 180 = 3(x – 12)
y = 33x – 396 + 180
y = 33x – 216

INTERpolating

Sekarang kita dapat menggunakan persamaan tersebut untuk interpolasi nilai penjualan di 21°:
y = 33 × 21° – 216 = $477

EXTRApolating

Dan untuk extrapolasi nilai penjualan di 29°:
y = 33 × 29° – 216 = $741

Nilai-nilai tersebut sangat dekat dengan apa yang kita peroleh pada grafik. Namun, tidak berarti mereka lebih akurat. Mereka hanya sebagai perkiraan.

Jangan gunakan extrapolation terlalu jauh! Apa penjualan yang kita harapkan di 0°?
y = 33 × 0° – 216 = -$216

Hmmm… Minus $216? Kita telah extrapolasi terlalu jauh!

Korelasi

Ketika dua set data sangat terkait, kita bilang bahwa mereka memiliki Korelasi Tinggi. Kata "Korelasi" terdiri dari Co- (berarti "bersama-sama") dan Relation.

Korelasi dapat berupa Korelasi Positif, di mana nilai-nilai meningkat bersama-sama, atau Korelasi Negatif, di mana salah satu nilai menurun saat nilai lainnya meningkat.

Contoh: Korelasi Negatif

Berikut adalah contoh korelasi negatif antara laju kelahiran dan penghasilan per orang:

Grafik scatter plot untuk sekitar 100 negara berbeda.
It has a negative correlation (the line slopes down)
Note: I tried to fit a straight line to the data, but maybe a curve would work better, what do you think?