Penggunaan regresi linier biasanya dianggap sebagai metode yang paling sederhana dan efektif untuk menganalisis hubungan antara variabel. Namun, dalam beberapa kasus, asumsi bahwa varian residuals konstan tidak lagi berlaku. Dalam kasus seperti itu, model regresi linier biasa dapat menghasilkan penaksiran parameter yang bias dan inferensi yang salah.

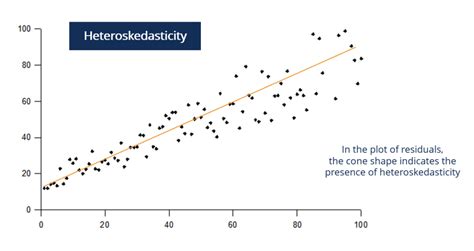
Heteroskedasticity Scatter Plot

Sebelum kita lanjut ke penggunaan metode hetregress, mari kita lihat bagaimana kita dapat mendeteksi heteroskedasticity dengan menggunakan scatter plot. Dalam scatter plot, kita dapat melihat apakah varian residuals berbeda untuk setiap level nilai variabel independen.

Heteroskedastic Linear Regression

Dalam Stata, kita dapat menggunakan perintah hetregress untuk menganalisis regresi linier dengan varian yang berbeda. Perintah ini memungkinkan kita untuk mengembangkan model yang dapat menangkap varian residuals yang tidak konstan.

Contoh Analisis

Mari kita lihat contoh analisis menggunakan data tentang prestasi siswa SMA (GPA) sebagai fungsi dari variabel independen, seperti tingkat kehadiran, level tahun pelajaran, partisipasi dalam olahraga, dan lain-lain. Dalam model ini, kita ingin mengembangkan model yang dapat menangkap varian residuals yang tidak konstan.

Model

Model regresi linier yang kita gunakan adalah:

GPA = β0 + β1 * Attendance + β2 * Grade Level + β3 * Sports + β4 * Extra Curricular Activities

Dalam model ini, kita juga ingin mengembangkan model untuk varian residuals yang tidak konstan. Model ini menggunakan eksponensial untuk mendeskripsikan varian residuals yang berbeda.

Hasil Analisis

Berikut adalah hasil analisis yang diperoleh dengan menggunakan perintah hetregress:

GPA Coefficients

• β0 = 0.7233421
• β1 = 0.0946848
• β2 = 1.558124 (for college level) dan 2.468524 (for graduate level)
• β3 = 0.7684617 (for yes#yes in ap#extra)
• β4 = -0.0339061 (for yes in extra curricular activities)

Variance Coefficients

• lnσ² = 0.7894325 (for college level) dan 1.9831641 (for graduate level)
• lnσ² = 1.765285 (for junior level) dan 2.539946 (for senior level)
• ap#extra = 0.1425211 (yes#yes)

Likelihood-Ratio Test

Berikut adalah hasil likelihood-ratio test yang menunjukkan bahwa model varian residuals yang tidak konstan lebih baik daripada model varian residuals yang konstan.

Dalam artikel ini, kita telah melihat bagaimana menggunakan perintah hetregress dalam Stata untuk menganalisis regresi linier dengan varian yang berbeda. Kita juga telah melihat contoh analisis menggunakan data tentang prestasi siswa SMA sebagai fungsi dari variabel independen. Dengan menggunakan metode ini, kita dapat mengembangkan model yang lebih baik dan menangkap varian residuals yang tidak konstan.