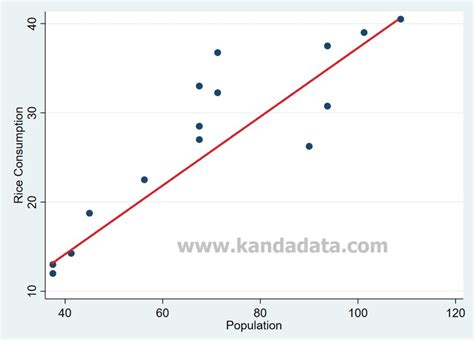
Dalam analisis statistik, scatterplots (grafik titik-titik) adalah salah satu cara untuk menampilkan hubungan antara variabel-variabel terkontinu. Namun, jika Anda ingin menggunakan contoh Anda untuk menginferkan karakteristik dari populasi keseluruhan, pastikan Anda melakukan uji hipotesis yang diperlukan dan mengevaluasi signifikansi statistik.

Grafik-grafik dapat subjektif karena software Anda memungkinkan Anda untuk memodifikasi sifat-sifat grafik, seperti skala grafik. Mengubah pengaturan-pengaturan ini dapat mengubah penampilan scatterplots dan kesimpulan yang Anda tarik dari mereka. Sebaliknya, uji hipotesis memberikan evaluasi objektif signifikansi statistik. Mereka juga mengakui kemungkinan error acak yang menjelaskan pola-pola dan perbedaan yang diamati.

Analisis Korrelasi dan Regresi

Korrelasi dan regresi adalah metode utama untuk mengevaluasi statistik hubungan antara data terkontinu.

Menginterpretasi Linear dan Nonlinear Relationships dari Scatterplots

Untuk menginterpretasi scatterplots, kita dapat menggunakan langkah-langkah berikut:

1. Berdasarkan titik-titik pada grafik, determinan apakah titik-titik konsisten meningkat atau menurun ketika kita bergerak sepanjang sumbu x.

2. Jika ada tren yang konsisten, lanjutkan ke langkah 2.

3. Jika tidak ada tren yang konsiste, scatterplot adalah nonlinear.

4. Berdasarkan titik-titik pada grafik, determinan apakah titik-titik umumnya mengikuti jalur lurus.

Jika titik-titik umumnya mengikuti jalur lurus, maka hubungan adalah linear.
Jika titik-titik tidak umumnya mengikuti jalur lurus, maka hubungan adalah nonlinear.

Contoh Menginterpretasi

Mari kita gunakan langkah-langkah di atas dan definisi-definisi untuk bekerja melalui tiga contoh menginterpretasi scatterplots yang linear dan nonlinear.

Contoh 1: Hubungan Linear
Grafik berikut menampilkan hubungan antara waktu belajar siswa untuk ujian matematika dan persentase yang mereka hasilkan.

Waktu Belajar vs Skor Ujian

Langkah 1: Berdasarkan titik-titik pada grafik, determinan apakah titik-titik konsisten meningkat atau menurun ketika kita bergerak sepanjang sumbu x.
Jika ada tren yang konsiste, lanjutkan ke langkah 2. Jika tidak ada tren yang konsiste, scatterplot adalah nonlinear.
Sebagai kita bergerak sepanjang sumbu x (jam belajar), titik-titik konsisten meningkat.

Langkah 2: Berdasarkan titik-titik pada grafik, determinan apakah titik-titik umumnya mengikuti jalur lurus.
Jika titik-titik umumnya mengikuti jalur lurus, maka hubungan adalah linear. Jika titik-titik tidak umumnya mengikuti jalur lurus, maka hubungan adalah nonlinear.
Titik-titik umumnya mengikuti jalur lurus. Oleh karena itu, terdapat hubungan linear antara waktu belajar dan skor ujian.

Contoh 2: Hubungan Nonlinear dengan Tren Konsiste
Grafik berikut menampilkan hubungan antara bakteri yang ada pada countertops dan waktu setelah disinfeksi countertop dengan bahan disinfektan. Berikan deskripsi grafik.

Waktu Disinfeksi vs Bakteri

Langkah 1: Berdasarkan titik-titik pada grafik, determinan apakah titik-titik konsisten meningkat atau menurun ketika kita bergerak sepanjang sumbu x.
Jika ada tren yang konsiste, lanjutkan ke langkah 2. Jika tidak ada tren yang konsiste, scatterplot adalah nonlinear.
Sebagai kita bergerak sepanjang sumbu x (jam setelah disinfeksi), titik-titik konsisten menurun.

Langkah 2: Berdasarkan titik-titik pada grafik, determinan apakah titik-titik umumnya mengikuti jalur lurus.
Jika titik-titik umumnya mengikuti jalur lurus, maka hubungan adalah linear. Jika titik-titik tidak umumnya mengikuti jalur lurus, maka hubungan adalah nonlinear.
Titik-titik tidak umumnya mengikuti jalur lurus. Oleh karena itu, terdapat hubungan nonlinear antara waktu setelah disinfeksi dan bakteri.

Contoh 3: Hubungan Nonlinear tanpa Tren
Grafik berikut menampilkan hubungan antara variabel A dan B. Berikan deskripsi grafik.

Variabel A vs Variabel B

Langkah 1: Berdasarkan titik-titik pada grafik, determinan apakah titik-titik konsisten meningkat atau menurun ketika kita bergerak sepanjang sumbu x.
Jika tidak ada tren yang konsiste, scatterplot adalah nonlinear.

Langkah 2: Berdasarkan titik-titik pada grafik, determinan apakah titik-titik umumnya mengikuti jalur lurus.
Jika titik-titik tidak umumnya mengikuti jalur lurus, maka hubungan adalah nonlinear.
Titik-titik tidak umumnya mengikuti jalur lurus. Oleh karena itu, terdapat hubungan nonlinear antara variabel A dan B.

Dalam artikel ini, kita telah mempelajari bagaimana menginterpretasi scatterplots untuk menentukan apakah hubungan antara dua variabel adalah linear atau nonlinear. Dengan menggunakan langkah-langkah yang tepat, kita dapat membuat kesimpulan yang lebih akurat tentang hubungan-hubungan statistik.