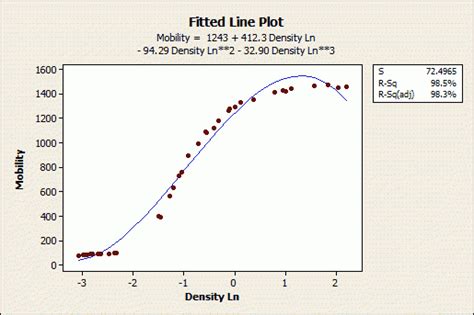
Dalam analisis statistik, koefisien determinasi (R-squared) digunakan untuk mengetahui kuatnya hubungan antara dua variable. R-squared adalah ukuran yang menjelaskan persentase variabilitas dari sebuah variable terhadap variable lainnya.
Contoh
Misalnya, kita ingin mengetahui seberapa besar pengaruh jumlah kuliah per hari terhadap jam orang tua habiskan di kampus per hari. Kita memiliki data sebagai berikut:
| Jumlah Kuliah | Jam Orang Tua di Kampus |
|---|---|
| 2 | 4 |
| 4 | 6 |
| 6 | 7 |
Dengan menggunakan rumus R-squared, kita dapat menghitung nilai R-squared sebagai berikut:
\begin{align} \text{Residual}&=\text{actual } y \text{ value} – \text{predicted }y \text{ value}\ r_4&=y_i-\hat{y_i}\ &=7-7.517\ &=-0.517 \end{align}
Untuk menentukan residuals squared, kita perlu menghitung setiap residuals dari $r_1$ hingga $r_4$ dan kemudian mencari jumlahnya.
\begin{align} \sum({y_i}-\hat{y_i})^2&=\sum{r_i}\ &={r_1}^2+{r_2}^2+{r_3}^2+{r_4}^2\ &=(−0.601)^2+(0.17)^2+(0.941)^2-(-0.517)^2\ &=1.542871 \end{align}
Untuk menentukan $\sum(y_i-\bar{y})^2$ kita perlu terlebih dahulu mencari rata-rata dari nilai $y$.
\begin{align} \bar{y}&=\frac{\sum{y}}{n}\ &=\frac{2+4+6+7}{4}\ &=\frac{19}{4}\ &=4.75 \end{align}
Sekarang kita dapat menghitung $\sum(y_i-\bar{y})^2$.
\begin{align} \sum(y_i-\bar{y})^2&=(2-4.75)^2+(4-4.75)^2+(6-4.75)^2+(7-4.75)^2\ &=(-2.75)^2+(-0.75)^2+(1.25)^2+(2.25)^2\ &=14.75 \end{align}
Jadi;
\begin{align} R^2&=1-\frac{\text{sum squared regression (SSR)} }{\text{total sum of squares (SST)} }\ &=1-\frac{\sum({y_i}-\hat{y_i})^2}{\sum(y_i-\bar{y})^2}\ &=1-\frac{1.542871}{14.75}\ &=1-0.105\ \text{(3.s.f)}\ &=0.895\text{ (3.s.f)} \end{align}
Artinya, jumlah kuliah per hari menjelaskan sekitar 89.5% dari variabilitas jam orang tua habiskan di kampus per hari.
Kesimpulan
R-squared adalah ukuran yang menjelaskan persentase variabilitas dari sebuah variable terhadap variable lainnya. Dalam contoh di atas, jumlah kuliah per hari menjelaskan sekitar 89.5% dari variabilitas jam orang tua habiskan di kampus per hari.
Referensi
Howell, D. C. (2013). Fundamental statistics for the behavioral sciences. Thomson Brooks/Cole.