Dalam analisis data, salah satu hal yang paling penting adalah mengetahui apakah data memiliki distribusi normal atau tidak. Hal ini sangat penting karena keterbatasan distribusi normal dapat mempengaruhi hasil analisis dan prediksi.

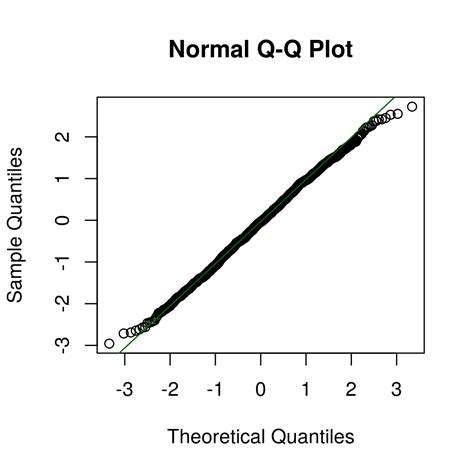
Salah satu cara untuk mengenal distribusi normal dari data adalah dengan menggunakan Q-Q plot (Quantile-Quantile plot). Q-Q plot adalah sebuah grafik yang menampilkan data dalam bentuk kuadrat melawan data dalam bentuk quantile. Jika data memiliki distribusi normal, maka titik-titik pada Q-Q plot akan berada di sekitar garis lurus.

Berikut ini adalah contoh bagaimana kita dapat membuat Q-Q plot menggunakan R:

QQplot <- function(x) {
 Quantile <- (c(1:length(x)) - 3/8) / (length(x) + 1/4)
 z <- qnorm(Quantile, 0, 1)
 x <- sort(x)
 return(plot(z, x, main = "QQplot"))
}

# Contoh data
data(iris)

x <- iris$Sepal.Length

par(mfrow = c(1, 2))
qqnorm(x)
QQplot(x)

Gambaran di atas menunjukkan bahwa R memiliki fungsi qqnorm dan QQplot yang dapat membantu kita membuat Q-Q plot. Namun, jika kita ingin membuat Q-Q plot sendiri, maka kita dapat menggunakan fungsi qnorm dan sort untuk menghasilkan Q-Q plot.

Selain itu, ada juga cara lain untuk mengetahui apakah data memiliki distribusi normal atau tidak, yaitu dengan menggunakan Shapiro Test. Shapiro Test adalah sebuah tes statistik yang digunakan untuk mengetahui apakah data memiliki distribusi normal atau tidak.

shapiro.test(x)

Hasil dari Shapiro Test dapat membantu kita mengetahui apakah data memiliki distribusi normal atau tidak.

Dalam contoh di atas, kita menggunakan fungsi shapiro.test dan hasilnya menunjukkan bahwa data Sepal.Length dari iris dataset memiliki p-value sebesar 0.01018, yang berarti data tersebut tidak memiliki distribusi normal (p-value < 0.05).

Dalam postingan ini, kita telah membahas beberapa cara untuk mengetahui apakah data memiliki distribusi normal atau tidak, yaitu dengan menggunakan Q-Q plot dan Shapiro Test. Kedua metode tersebut dapat membantu kita mengetahui apakah data memiliki distribusi normal atau tidak, sehingga kita dapat membuat prediksi yang lebih akurat.

Namun, dalam analisis data, kita juga harus mempertimbangkan beberapa hal lainnya, seperti jenis data, jumlah data, dan keterbatasan distribusi. Oleh karena itu, dalam postingan selanjutnya, kita akan membahas lebih lanjut tentang cara-cara untuk mengetahui apakah data memiliki distribusi normal atau tidak.