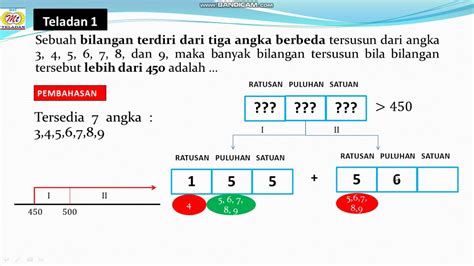
Anda mungkin pernah melihat orang-orang mengenakan baju, celana, dan topi dengan berbagai cara. Ternyata, jumlahnya tidak sedikit. Misalnya, Andi mempunyai kemeja berwarna biru, merah, putih, serta batik, dan celana berwarna hitam, biru, dan coklat. Tentukan kemungkinan pasangan yang dapat terjadi dan berapa banyaknya pasangan yang dapat terjadi?
Pertama-tama, kita akan membuat tabel untuk melihat semua kemungkinan pasangan:
| Kemeja | Celana |
|---|---|
| Biru (B) | Hitam (HB), HB, HP, HK |
| Merah (M) | HB, HM, HP, HK, BM, BP, BK, CM, CP, CK |
| Putih (P) | HB, HP, HK, BP, BK, CP, CK |
| Batik (K) | HB, HP, HK, BK, CP, CK |
Dengan melihat tabel di atas, kita dapat mengetahui bahwa jumlah pasangan yang dapat terjadi adalah 12. Ternyata, Andi mempunyai 12 pasang kemeja dan celana yang berbeda.
Jalan untuk Sampai dari Kota A ke Kota C
Kita juga dapat menemukan banyak cara untuk sampai dari Kota A ke Kota C melalui jalan yang tersedia. Misalnya, terdapat 3 buah jalan untuk sampai dari Kota A ke Kota B dan 7 buah jalan dari Kota B ke Kota C.
Jika Parman yang tinggal di Kota A ingin mengunjungi saudaranya yang tinggal di Kota C, banyak cara Parman untuk sampai di Kota C adalah:
- Dari Kota A ke Kota B melalui Jalan 1, lalu dari Kota B ke Kota C melalui Jalan 2
- Dari Kota A ke Kota B melalui Jalan 2, lalu dari Kota B ke Kota C melalui Jalan 3
- Dari Kota A ke Kota B melalui Jalan 3, lalu dari Kota B ke Kota C melalui Jalan 4
- Dari Kota A ke Kota B melalui Jalan 1, lalu dari Kota B ke Kota C melalui Jalan 5
- Dari Kota A ke Kota B melalui Jalan 2, lalu dari Kota B ke Kota C melalui Jalan 6
- Dari Kota A ke Kota B melalui Jalan 3, lalu dari Kota B ke Kota C melalui Jalan 7
Dengan demikian, Parman memiliki 6 cara untuk sampai di Kota C.
Bilangan Dua Digit Kelipatan Lima
Kita juga dapat menemukan banyak bilangan dua digit kelipatan lima yang dapat dibuat dari angka 0,1,3,4,5,7,9. Misalnya:
15, 25, 35, 45, 55, 70, 75, 85, 95
Dengan demikian, jumlah bilangan dua digit kelipatan lima yang dapat dibuat adalah 9.
Bilangan Dua Digit Genap
Kita juga dapat menemukan banyak bilangan dua digit genap yang dapat dibuat dari angka 1,3,4,5,7,8. Misalnya:
10, 12, 14, 16, 18, 20, 22, 24, 26
Dengan demikian, jumlah bilangan dua digit genap yang dapat dibuat adalah 9.
Bilangan Tiga Digit
Kita juga dapat menemukan banyak bilangan tiga digit yang kurang dari 300 yang dapat dibuat dari angka 0,1,2,3,4,5,6. Misalnya:
100, 101, 102, …, 299
Dengan demikian, jumlah bilangan tiga digit yang kurang dari 300 adalah 200.
Suatu Perkumpulan Basket
Kita juga dapat menemukan banyak cara untuk memilih susunan pemain basket dari 9 orang atlet. Misalnya:
- Pilih 5 orang pertama: A, B, C, D, E
- Pilih 5 orang kedua: F, G, H, I, J
- Pilih 5 orang ketiga: K, L, M, N, O
Dengan demikian, jumlah cara untuk memilih susunan pemain basket adalah 3.
Itulah beberapa contoh dari banyak cara yang dapat kita temukan dalam kehidupan sehari-hari. Dengan menggunakan konsep dasar matematika seperti tabel, grafik, dan rumus, kita dapat menemukan berbagai jawaban untuk masalah yang kita hadapi.