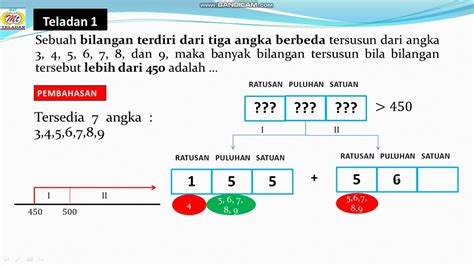
Dalam matematika, konsep filling slots atau menyusun nilai tempat adalah suatu teknik untuk membuat bilangan-bilangan ganjil dan kurang dari 500. Dalam artikel ini, kita akan membahas bagaimana cara menentukan banyaknya bilangan ganjil yang dapat disusun dan bilangan kurang dari 500.

Banyak Bilangan Ganjil yang Dapat Disusun

Soal pertama adalah mencari banyaknya bilangan ganjil yang dapat disusun. Untuk itu, kita perlu menentukan bagaimana cara angka-angka menempati tiga tempat berikut: kotak ketiga, kotak pertama, dan kotak kedua.

Kotak ketiga harus diisi oleh sebuah bilangan ganjil, sehingga hanya dapat diisi oleh angka 5, 7, dan 9. Maka, P3 = 3.

Kotak pertama dapat diisi oleh banyak angka yang tersedia dikurang satu karena sudah ada satu angka yang digunakan pada kotak ketiga. Maka, P1 = 6 – 1 = 5.

Kotak kedua dapat diisi oleh banyak angka yang tersedia dikurang dua karena sudah ada dua angka yang digunakan pada kotak ketiga dan pertama. Maka, P2 = 6 – 2 = 4.

Dengan demikian, banyaknya bilangan ganjil yang dapat disusun adalah P1 × P2 × P3 = 5 × 4 × 3 = 60 bilangan. Jadi, banyak bilangan ganjil yang dapat disusun adalah 60 bilangan.

Banyak Bilangan Kurang dari 500

Soal kedua adalah mencari banyaknya bilangan kurang dari 500 yang terbentuk dengan menggunakan filling slots. Dalam soal ini, kita diminta untuk membuat bilangan ganjil yang terdiri dari tiga digit berbeda.

Kotak ketiga harus diisi oleh sebuah bilangan ganjil, sehingga hanya dapat diisi oleh angka 5 dan 9. Maka, P3 = 2.

Kotak pertama dapat diisi oleh banyak angka yang tersedia dikurang dua karena sudah ada dua angka yang digunakan pada kotak ketiga dan kedua. Maka, P1 = 2 (karena bilangan kurang dari 500).

Kotak kedua dapat diisi oleh semua angka yang tersedia, yaitu 6, dikurang dua karena sudah ada tiga angka yang digunakan pada kotak pertama, ketiga, dan kedua. Maka, P2 = 4.

Dengan demikian, banyaknya bilangan kurang dari 500 adalah P1 × P2 × P3 = 2 × 4 × 2 = 16 bilangan. Jadi, banyak bilangan yang terbentuk yang nilainya kurang dari 500 adalah 16 bilangan.

Kesimpulan

Dalam artikel ini, kita telah membahas bagaimana cara menentukan banyaknya bilangan ganjil yang dapat disusun dan bilangan kurang dari 500 menggunakan filling slots. Kita juga telah melihat contoh soal-soal yang terkait dengan konsep ini. Semoga artikel ini bermanfaat bagi Anda!