Here are the articles in Indonesian:

Case Analysis

Saat ini, kita akan melakukan analisis kasus: Kasus 1: Titik A memiliki satu anak, yang kita denote sebagai titik B. Dalam kasus ini, kita hapus titik A dan kita memiliki sebuah pohon biner akar dengan titik B sebagai akar; mari kita sebut tree T0. Mudah untuk melihat bahwa tinggi T0 sama dengan N. Kita menggunakan hipotesis induktif pada tree T0, yang menyatakan ukuran T0 tidak lebih dari… Kita memiliki bahwa… Kami perhatikan dalam ketentuan ketujuh di atas, kita menggunakan fakta bahwa untuk setiap N ≥ 0, kita memiliki bahwa… Kita mengkonklusikan bahwa pernyataan ini benar dalam kasus ini.

Kasus 2: Titik A memiliki dua anak, titik B dan C (seperti contoh gambar di atas). Kita lagi hapus titik A dan kita memiliki dua pohon biner akar, satu yang berakar pada titik B dan lainnya yang berakar pada titik C. Mari kita sebut tree T1 sebagai pohon biner yang berakar pada titik B dan tree T2 sebagai pohon biner yang berakar pada titik C. Mudah untuk melihat bahwa baik T1 maupun T2 memiliki tinggi tidak lebih dari N. Kita menggunakan hipotesis induktif pada kedua pohon, yang memberikan kita… Kita memiliki bahwa… Kami mengkonklusikan lagi bahwa pernyataan ini benar dalam kasus ini.

Untuk menyelesaikan bukti, kita perhatikan bahwa kita tidak membuat asumsi tentang tree T, dan oleh karena itu pernyataan di atas benar untuk setiap pohon tinggi N + 1. Kita selesai!

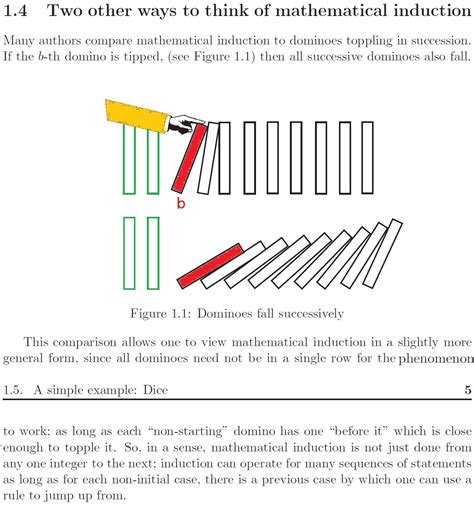
Analogi Induksi Matematika

Sementara analogi yang dituju adalah tentang dominonya ideal yang ditempatkan secara sempurna dalam lingkungan sempurna, namun induksi matematika gagal jika asumsi kesempurnaan salah.
Contoh, pertimbangkan bukti induktif bahwa x + 1 > x. Karena batasan fisik, pada banyak environment programming integer overflow dapat terjadi. https://en.m.wikipedia.org/wiki/Integer_overflow
Pada layar dengan maksimum enam digit, 999999 diikuti oleh 000000. Contoh ini adalah contoh pasangan dominonya yang sangat berbeda dari pasangan lainnya. Jadi, konsern Anda tentang analogi tidak salah, tetapi biasanya tidak relevan untuk bukti matematika.

Penggunaan Induksi Kuat

Prove that the first player has a winning strategy for the game of Chomp, introduced in Example 12 in Section 1.8, if the initial board is two squares wide, that is, a 2x n board. [Hint: Use strong induction. The first move of the first player should be to Chomp the cookie in the bottom row at the far right.]

Prove that if x and y are real numbers with x < y, then there is a rational number r with x < r < y. [Hint: Use the Archimedean property, given in Appendix 1, to find a positive integer A with .A > 1/(y-x) Then show that there is a rational number with denominator A between x and y by looking at the numbers ⌊x⌋ + j/A, where is a positive integer.]

Let P(n) be the statement that a postage of n cents can be formed using 4-cent stamps and 7-cent stamps. The parts of this exercise outline a strong induction proof that P(n) is true for n ≥ 18.

(a) Show statements P(18), P(19), P(20), and P(32) are true, completing the basis step of the proof.

(b) What is the inductive hypothesis of the proof?

(c) What do you need to prove in this inductive step?

(d) Complete the inductive step for k ≥ 21.

(e) Explain why these steps show that statement is true whenever