SMALL Function Syntax
SMALL ($B$1:$B$12, 1)
The syntax and pass-on value are the same. Now when we use this function in the above example, we will get the following output:
Note: If there are multiple outliers in the data then you have to use the function again and again.
Finding Outliers using Inter Quartile Range(IQR)
Data presented in the above example has a small sample size but when it comes to a real-life situation, the data can be huge, and that’s where the original problem arrives. As per IQR, An outlier is any point of data that lies over 1.5 times IQRs below the first quartile (Q1) and 1.5 times IQR above the third quartile (Q3) in a data set.
Formula
High = Q3 + 1.5 * IQR
Low = Q1 – 1.5 * IQR
Finding Outliers using the following steps:
Step 1: Open the worksheet where the data to find outlier is stored.
Step 2: Add the function QUARTILE(array, quart), where an array is the data set for which the quartile is being calculated and a quart is the quartile number. In our case, the quart is 1 because we wish to calculate the 1st quartile to calculate the lowest outlier.
Quart Number | Quartile Returns
| Number | Quartile Returns |
|---|---|
| 0 | Minimum Value |
| 1 | First quartile (25th percentile) |
| 2 | Median Value (50th percentile) |
| 3 | Third Quartile (75th percentile) |
| 4 | Maximum Value |
Step 3: Similar to step 2, add the quartile formula under Q3 and write 3 as quart number because we wish to calculate the 3rd quartile i.e. 75th percentile to calculate the highest quartile value.
Step 4: Inter Quartile Range or IQR is Q3-Q1, put the formula to get the IQR value.
Step 5: To find the High value, the formula is Q3+(1.5IQR). Similarly, for Low value, the formula is Q1-(1.5IQR)
Step 6: To find whether the number in the data set is an outlier or not, we need to check whether the data entry is higher than the High value or lower than the Low value. To perform this we will use the OR function. The formula will be OR(B3>$G$3, B3<$H$3). Put the formula in the required cell and drag down the cell adjacent to the last data set, if the value returns TRUE, then the data is an outlier otherwise not.
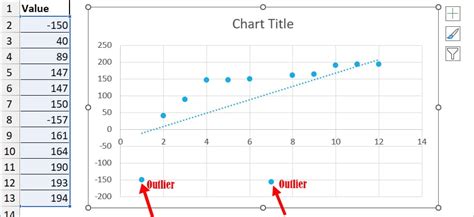
Outliers in Scatter Plots
What are outliers in scatter plots? Scatter plots often have a pattern. We call a data point an outlier if it doesn't fit the pattern.
Consider the scatter plot above, which shows data for students on a backpacking trip. (Each point represents a student.) Notice how two of the points don't fit the pattern very well. These points have been labeled Brad and Sharon, which are the names of the students they represent.
Sharon could be considered an outlier because she is carrying a much heavier backpack than the pattern predicts. Brad could be considered an outlier because he is carrying a much lighter backpack than the pattern predicts.
Key idea: There is no special rule that tells us whether or not a point is an outlier in a scatter plot. When doing more advanced statistics, it may become helpful to invent a precise definition of "outlier", but we don't need that yet.
Practice problems
To fully wrap our minds around why certain data points might be considered outliers, let's try a couple of practice problems.
Problem 1: Computer shopping
Michelle was researching different computers to buy for college. She looked up the prices and quality ratings for a sample of computers. Her data is shown in the scatter plot to the right, where each point is a computer.
Problem 2: Test scores
Some high school students in the U.S. take a test called the SAT before applying to colleges. The scatter plot to the right shows what percent of each state's college-bound graduates took the SAT in 2009-2010, along with that state's average score on the math section.
The three labeled points could be considered outliers.