Scatter plots are a powerful tool in statistics that allow us to visualize the relationship between two variables. In this article, we will explore the concept of scatter plots, its limitations, and how to interpret the results.
What is a Scatter Plot?
A scatter plot is a graph that shows the relationship between two variables. It is commonly used to identify patterns or correlations between variables. To use a scatter plot, the data must be in an interval or ratio scale.
Example of a Scatter Plot
In the following example (Figure 1), we can see a scatter plot of the percentage of car ownership and household income in the United States. The graph shows that as the percentage of car ownership increases, so does the household income.
Interpreting the Results
There are several ways to interpret the results of a scatter plot:
- Linear Relationship: If the data points form a straight line, it indicates a strong linear relationship between the two variables (Figure 2).
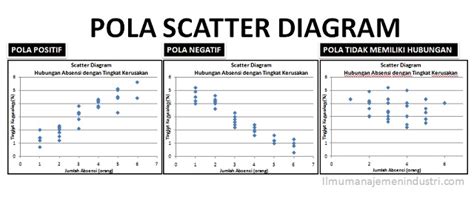
- Positive Linear Relationship: If the data points increase as they move from left to right, it indicates a positive linear relationship between the two variables (Figure 3). In this case, an increase in one variable is accompanied by an increase in the other.
- Negative Linear Relationship: If the data points decrease as they move from left to right, it indicates a negative linear relationship between the two variables (Figure 4). In this case, an increase in one variable is accompanied by a decrease in the other.
- No Relationship: If the data points are randomly scattered and do not show any pattern or trend, it indicates no significant relationship between the two variables (Figure 5).
- Non-Linear Relationship: If the data points form a curve or non-linear shape, it indicates a non-linear relationship between the two variables (Figure 6).
Limitations of Scatter Plots
While scatter plots are a powerful tool for identifying relationships between variables, they also have some limitations:
- Sample Size: Scatter plots can be misleading if the sample size is small (less than n=30). This is because small samples can lead to false patterns or correlations.
- Outliers: Scatter plots can also be affected by outliers, which are extreme data points that may not be representative of the overall trend.
****, scatter plots are a valuable tool for identifying relationships between variables. By understanding how to interpret the results and recognizing its limitations, we can use scatter plots to gain insights into the behavior of our variables.