Heteroskedastisitas adalah salah satu masalah yang umum terjadi dalam analisis regresi linear. Heteroskedastisitas adalah keanehan variance dari residual, yang berarti bahwa residu memiliki variasi yang tidak sama untuk setiap observasi.
Uji Heteroskedastisitas dengan Chi-Square
Satu-satunya cara untuk mengetahui apakah terdapat heteroskedastisitas atau tidak adalah dengan menggunakan uji statistik. Salah satu uji yang paling populer digunakan untuk mengidentifikasi heteroskedastisitas adalah uji chi-square.
Dalam analisis regresi linear, kita dapat menggunakan uji chi-square untuk mengetahui apakah terdapat hubungan antara nilai prediksi variabel independen (Zpred) dan residu (SRESID). Jika nilai signifikansi < 0.05, maka dapat disimpulkan bahwa terdapat heteroskedastisitas.
Uji Glejser
Uji Glejser adalah salah satu uji yang paling populer digunakan untuk mengidentifikasi heteroskedastisitas. Uji ini dilakukan dengan meregresikan variabel-variabel bebas terhadap nilai absolut residualnya (Gujarati, 2004).
Uji ARCH
Uji ARCH (Autoregressive Conditional Heteroskedasticity) adalah salah satu uji yang paling populer digunakan untuk mengidentifikasi heteroskedastisitas. Uji ini dilakukan dengan meregresikan variabel-variabel bebas terhadap nilai signifikansi variabel independen.
Cara Mengidentifikasi Heteroskedastisitas dengan Grafik Scatterplot
Selain menggunakan uji statistik, kita juga dapat mengidentifikasi heteroskedastisitas dengan menggunakan grafik scatterplot. Grafik scatterplot SPSS adalah melihat grafik scatterplot antara nilai prediksi variabel independen (Zpred) dengan residunya (SRESID).
Jika terdapat pola tertentu pada grafik scatterplot, seperti titik-titik yang membentuk pola yang teratur (bergelombang, menyebar kemudian menyempit), maka dapat disimpulkan bahwa telah terjadi heteroskedastisitas. Sebaliknya, jika tidak ada pola yang jelas, serta titik-titik menyebar, maka indikasinya adalah tidak terjadi heteroskedastisitas.
Contoh
Misalnya kita punya data seperti di bawah ini X1, X2 dan Y. Model yang akan diuji adalah pengaruh X1 dan X2 terhadap Y.
Buka Aplikasi SPSS anda, copy-paste 3 variabel di atas ke SPSS. Kemudian buat 3 variabel dengan skala data “Scale” Type “Numeric” Decimal “2” dengan nama sesuai tabel di atas: X1, X2 dan Y.
Klik Menu > Analyze > Regression > Linear, masukkan variabel X1 dan X2 ke independent, Y ke dependen. Klik Plots, sehingga muncul jendela “Linear Regression Plots”. Kemudian masukkan SRESID pada kotak Y dan ZPRED pada kotak X, klik Continue dan Klik OK.
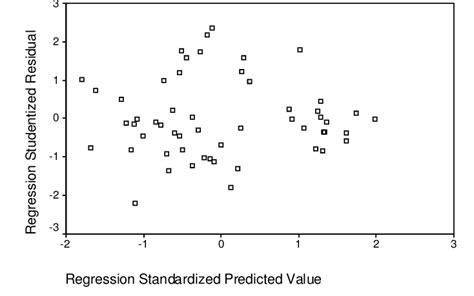
Output yang dihasilkan dalam uji heteroskedastisitas dengan grafik scatterplot
Lihat Grafik Scatter di atas, jelas bahwa tidak ada pola tertentu karena titik-titik menyebar tidak beraturan di atas dan di bawah sumbu 0 pada sumbu Y. Maka dapat disimpulkan tidak terdapat gejala heteroskedastisitas atau H0 diterima.
Referensi
Juliandi A, Irfan, Manurung S. 2014. Metodologi Penelitian Bisnis: Konsep dan Aplikasi. Medan: UMSU Press.
Ghozali, I. (2016) Aplikasi Analisis Multivariete Dengan Program IBM SPSS 23. Edisi 8. Semarang: Badan Penerbit Universitas Diponegoro.
Gujarati, Damodar N, (2004). Basic Econometrics, Fourth edition, Singapore. McGraw-Hill Inc.
Kesimpulan
Heteroskedastisitas adalah salah satu masalah yang umum terjadi dalam analisis regresi linear. Cara mengidentifikasi heteroskedastisitas dengan grafik scatterplot SPSS adalah melihat grafik scatterplot antara nilai prediksi variabel independen (Zpred) dengan residunya (SRESID). Jika terdapat pola tertentu pada grafik scatterplot, maka dapat disimpulkan bahwa telah terjadi heteroskedastisitas. Sebaliknya, jika tidak ada pola yang jelas, serta titik-titik menyebar, maka indikasinya adalah tidak terjadi heteroskedastisitas.
Lampiran
Grafik Scatter SPSS:

Daftar Pustaka
Juliandi A, Irfan, Manurung S. 2014. Metodologi Penelitian Bisnis: Konsep dan Aplikasi. Medan: UMSU Press.
Ghozali, I. (2016) Aplikasi Analisis Multivariete Dengan Program IBM SPSS 23. Edisi 8. Semarang: Badan Penerbit Universitas Diponegoro.
Gujarati, Damodar N, (2004). Basic Econometrics, Fourth edition, Singapore. McGraw-Hill Inc.
Terima Kasih
Kami berterima kasih telah membaca artikel ini. Kami berharap artikel ini dapat memberikan informasi yang bermanfaat bagi Anda dalam mengidentifikasi heteroskedastisitas dalam regresi linear.