Pendidikan dan penghasilan memiliki hubungan yang erat. Pendidikan memainkan peranan penting dalam meningkatkan kemampuan seseorang untuk mendapatkan pekerjaan dengan gaji tinggi. Namun, apakah hubungan antara pendidikan dan penghasilan seimbang? Dalam analisis regresi, homoskedastisitas adalah asumsi yang penting untuk menjamin keandalan prediksi.
Skenario Homoskedastisitas
Dalam skenario homoskedastisitas, residu memperlihatkan penyebaran uniform di atas berbagai tingkat pendidikan. Irrespektif jumlah tahun pendidikan, variabilitas error tetap stabil. Dalam visualisasinya:
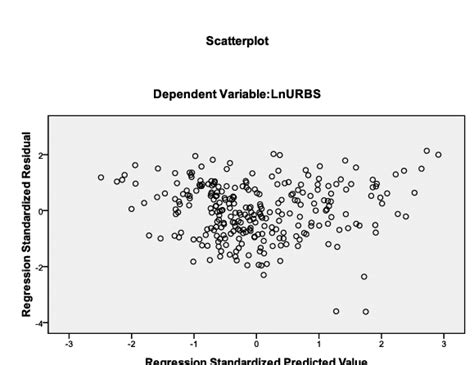
- Plot Residu vs Fitted Values
Pemeriksaan plot tersebut menunjukkan scatter random titik-titik tanpa pola yang jelas. Penyebaran titik-titik mempertahankan pola konsisten di atas seluruh rentang nilai yang diprediksi.
Skenario Heteroskedastisitas
Sekarang, mari kita telusuri skenario di mana heteroskedastisitas mengganggu asumsi homoskedastisitas.
- Plot Residu vs Fitted Values
Dalam kasus ini, plot tersebut mungkin menampilkan pola yang jelas, mungkin berbentuk kerucut atau lonceng. Contohnya, individu dengan tingkat pendidikan rendah dapat menunjukkan penyebaran residu yang sempit, yang menandakan variasi rendah. Sebaliknya, mereka dengan tingkat pendidikan lebih tinggi dapat menampilkan penyebaran residu yang lebar, yang menandakan variasi yang lebih besar.
Pentingnya Homoskedastisitas
- Efisiensi Estimasi
Homoskedastisitas memastikan bahwa estimasi koefisien regresi adalah efisiensi, memiliki varian minimal.
- Validitas Inference
Keluaran dari asumsi homoskedastisitas dapat mengintroduksi biasa terhadap standard error, yang mempengaruhi validitas inference statistik seperti uji hipotesis dan interval kepercayaan.
- Reliability Model
Model homoskedastisitas lebih andal untuk membuat prediksi di atas seluruh rentang variabel independen. Sebaliknya, model heteroskedastisitas mungkin menghasilkan prediksi yang kurang akurat untuk subset tertentu data.
- Penanganan Heteroskedastisitas
Jika heteroskedastisitas dikenali, potensi penawaran termasuk transformasi variabel, penggunaan weighted least squares regresi, atau eksplorasi model regresi yang resisten terhadap heteroskedastisitas.
Cara Mengetahui Homoskedastisitas
Berbagai metode dapat digunakan untuk mengetahui homoskedastisitas dalam analisis regresi:
- Plot Residu vs Fitted Values
Buat plot scatter yang menggabungkan nilai diprediksi (fitted) pada sumbu x dan residu pada sumbu y.
Homoskedastisitas ditunjukkan oleh penyebaran titik-titik yang konsisten di atas semua tingkat nilai diprediksi, tanpa pola seperti "fan" shape yang menandakan variasi perubahan.
- Plot Residu vs Variabel Independen
Buat plot scatter untuk masing-masing variabel independen dengan residu pada sumbu y.
Absensi pola atau trend dalam plot tersebut menunjukkan homoskedastisitas.
- Scale-Location Plot (Square Root of Residuals)
Buat plot yang serupa dengan plot residu vs fitted values, tetapi menggunakan akar kuadrat absolut residu pada sumbu y.
Plot ini bermanfaat untuk mempertegas pola, jika ada.
- Test Breusch-Pagan
Eksekusi test statistik formal dengan menggabungkan residu pada sumbu x dan variabel independen pada sumbu y.
P-value tidak signifikan (misalnya > 0,05) mendukung hipotesis nol homoskedastisitas.
- Test Goldfeld-Quandt
Lakukan test dengan membagi data menjadi sub-group berdasarkan variabel terpilih, kemudian menggabungkan residu pada sumbu x dan variabel independen pada sumbu y.
P-value tidak signifikan (misalnya > 0,05) mendukung hipotesis nol homoskedastisitas.
Dalam analisis regresi, homoskedastisitas adalah asumsi yang penting untuk menjamin keandalan prediksi. Dengan memahami konsep ini dan cara mengetahui homoskedastisitas, kita dapat membuat prediksi yang lebih akurat dan andal.