Dalam analisis statistika, regresi linier adalah metode yang digunakan untuk menentukan hubungan antara dua variable atau lebih. Dalam kasus ini, kita akan menggunakan grafik dan metode numerik untuk mendapatkan persamaan regresi linier.

Menggunakan Grafik

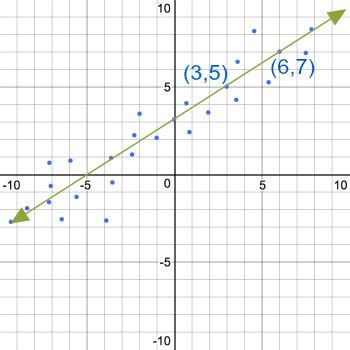
Langkah pertama dalam membuat analisis regresi linier adalah dengan membuat scatter plot dari data yang tersedia. Scatter plot adalah grafik yang digunakan untuk menampilkan hubungan antara dua variable. Dalam kasus ini, kita akan menggunakan data yang berupa pasangan nilai x dan y.

Selanjutnya, kita perlu menentukan sumbu-x dan sumbu-y dengan judul yang tepat. Setelah itu, kita dapat memplot masing-masing titik data dalam grafik. Keterkaitan antara data set yang diplot akan tampak jelas sekarang.

Garis Terbaik

Setelah membuat scatter plot, kita dapat menggunakan metode grafik untuk mendapatkan persamaan regresi linier. Langkah pertama adalah dengan menarik garis terbaik melalui semua titik data. Garis ini harus sejajar dengan kemungkinan bahwa ada jumlah titik di atas garis dan jumlah titik di bawah garis.

Setelah garis terbaik dibuat, kita dapat menggunakan metode standar untuk mendapatkan persamaan regresi linier.

Persamaan Regresi Linier

Persamaan regresi linier adalah sebagai berikut: y = mx + c, where m adalah kemiringan garis dan c adalah titik potong sumbu-y. Untuk mendapatkan nilai m, kita dapat menggunakan dua titik yang ada pada garis. Dalam kasus ini, kita akan asumsikan bahwa dua titik tersebut adalah (1,3) dan (0,1). Nilai m dapat dihitung dengan menghitung perbedaan koordinat-y dan membagi dengan perbedaan koordinat-x: m = (3-1)/(1-0) = 2.

Dengan demikian, persamaan regresi linier adalah y = 2x + c. Nilai c dapat dihitung dengan menggantikan nilai titik yang diketahui ke dalam persamaan dan menyesuaikan untuk mencari nilai c: 3 = (2 × 1) + c -> c = 3-2 = 1.

Metode Numerik

Ada beberapa metode numerik yang dapat digunakan untuk mendapatkan regresi linier, termasuk metode least squares. Metode least squares adalah sebagai berikut:

1. Hitung jumlah nilai-x: x_sum = 4.1 + 6.5 + 12.6 = 23.2
2. Hitung jumlah nilai-y: y_sum = 2.2 + 4.4 + 10.4 = 17
3. Hitung produk setiap pasangan data: xy_sum = (4.1 × 2.2) + (6.5 × 4.4) + (12.6 × 10.4) = 168.66
4. Hitung jumlah nilai-x persegi dan nilai-y persegi: x^2_sum = (4.1^2) + (6.5^2) + (12.6^2) = 217.82, y^2_sum = (2.2^2) + (4.5^2) + (10.4^2) = 133.25
5. Hitung jumlah titik data: N = 3

Dengan demikian, persamaan regresi linier dapat dihitung sebagai berikut:

m = ((N × xy_sum) – (x_sum × y_sum)) / ((N × x^2_sum) – (x_sum × x_sum)) -> m = (3 × 168.66) – (23.2 × 17) / (3 × 217.82) – (23.2 × 23.2) -> m = 0.968

c = ((x^2_sum × y_sum) – (x_sum × xy_sum)) / ((N × x^2_sum) – (x_sum × x_sum)) -> c = (217.82 × 17) – (23.2 × 168.66) / (3 × 217.82) – (23.2 × 23.2) -> c = -1.82

Persamaan regresi linier yang diperoleh adalah: y = 0.968x – 1.82