Pengumpulan data crossection seringkali mengandung situasi heteroskedastisitas karena data ini menghimpun data yang mewakili berbagai ukuran kecil, sedang, dan besar (Ghozali, 2016). Residual adalah selisih antara nilai observasi dengan nilai prediksi; dan absolut adalah nilai mutlak. Apabila variasi residual dari suatu pengamatan ke pengamatan lainnya tetap, maka hal tersebut dinamakan homokedastisitas. Sedangkan apabila variasi residualnya berbeda, maka dinamakan heterokedastisitas.

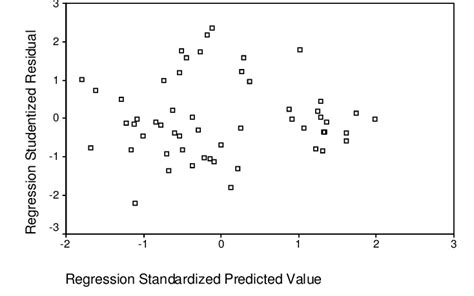
Untuk deteksi ada atau tidaknya heteroskedastisitas dalam suatu model regresi linear berganda, maka dilakukan dengan melihat grafik scatterplot atau nilai prediksi variabel terikat yang disebut SRESID dengan residual error ZPRED. Grafik scatterplot dapat membantu untuk menentukan apakah ada pola tertentu yang mengindikasikan adanya heteroskedastisitas.

Dasar pengambilan keputusan sebagai berikut:

• Jika terdapat pola tertentu seperti titik-titik yang ada membentuk pola tertentu yang teratur (bergelombang, melebar kemudian menyempit), maka mengindikasikan bahwa terjadi heteroskedastisitas.
• Jika tidak terdapat pola yang jelas, maupun titik-titik yang menyebar di atas dan di bawah angka 0 pada sumbu y, maka tidak terjadi heteroskedastisitas.

Jika tidak terdapat adanya titik – titik yang membentuk pola tertentu yang teratur, dan titik – titik pada scatterplot di atas menyebar secara acak di atas maupun di bawah angka 0 pada sumbu y. Hal tersebut artinya menunjukkan bahwa tidak terjadi masalah heteroskedastisitas.

Solusi jika model menyalahi asumsi heteroskedastisitas adalah dengan mentransformasikan ke dalam bentuk logaritma, yang hanya dapat dilakukan jika semua data bernilai positif. Atau dapat juga dilakukan dengan membagi semua variabel dengan variabel yang mengalami gangguan heteroskedastisitas.

Selain itu, dapat juga dilakukan uji statistik lainnya seperti Uji Breusch-Pagan dan Uji Glejser untuk mengetahui adanya heteroskedastisitas.

Uji Breusch-Pagan. Kriteria pengambilan keputusan dari uji Breusch-Pagan adalah sebagai berikut:

• Jika nilai signifikansi > 0,05 , maka tidak terjadi heteroskedastisitas
• Jika nilai signifikansi < 0,05 , maka terjadi heteroskedastisitas

Dalam penelitian ini, chi Square dari Obs*R-Squared adalah sebesar 0.1493 sehingga lebih besar daripada nilai alpha (0.05) yaitu (0.1493 > 0.05). Jika melebihi dari nilai alpha (0.05) dapat diartikan bahwa data terbebas dari masalah heteroskedastitas.

Uji Glejser. Uji Glejser dilakukan dengan meregresikan variabel-variabel bebas terhadap nilai absolut residualnya (Gujarati, 2004).

Uji ARCH. Dasar pengambilan keputusan dari uji ARCH adalah sebagai berikut:

• Jika nilai signifikan variabel independen < 0,05 maka terjadi Heterokedastisitas
• Jika nilai signifikan variabel independen > 0,05 maka tidak terjadi Heterokedastisitas

Dalam penelitian ini, uji ARCH juga menunjukkan bahwa tidak terjadi heteroskedastisitas.

Referensi:

Juliandi A, Irfan, Manurung S. 2014. Metodologi Penelitian Bisnis: Konsep dan Aplikasi. Medan: UMSU Press.
Ghozali, I. (2016) Aplikasi Analisis Multivariete Dengan Program IBM SPSS 23. Edisi 8. Semarang: Badan Penerbit Universitas Diponegoro.
Gujarati, Damodar N, (2004). Basic Econometrics, Fourth edition, Singapore. McGraw-Hill Inc.

Image Sources: Google Images