When we analyze a scatter plot, it's not just about visualizing the relationship between two variables. We can also gain valuable insights by incorporating confidence intervals into our analysis.

A confidence interval is an estimate of the population parameter (in this case, the conditional mean) that has a certain probability (usually 95%) of containing the true value. In other words, it's like wrapping ourselves in a safety net to ensure we're not just looking at one data point, but rather considering the uncertainty involved in our estimation.

How to Interpret Confidence Intervals

One popular method for interpreting confidence intervals is to consider values that are compatible with the observed data. Think of it this way: if you were to repeat the experiment many times, the 95% confidence interval would contain the true conditional mean approximately 95% of the time.

To illustrate this, let's say we're interested in estimating the conditional mean of y given x = x0. Our estimate might change from sample to sample (because our sample changes), but if we repeated the experiment ad infinitum and computed the confidence intervals, then on average 95% of them would contain the true conditional mean β0 + β1x.

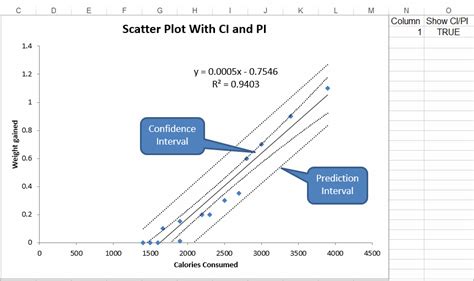
Scatter Plot with Confidence Intervals and Prediction Intervals

QI Macros makes it easy to draw scatter plots with both confidence intervals (CI) and prediction intervals (PI). CI provides a view into the uncertainty when estimating the mean, while PI accounts for variation in the Y values around the mean.

Here's how you can create these charts using QI Macros:

1. Select your data, then select Scatter Plot from QI Macros menu.
2. QI Macros will perform all calculations and create a scatter plot with a trend line and lines for the confidence interval and prediction interval.
3. You can also display calculations for the correlation of determination.

How to Create Confidence Intervals with plt.fill_between

Let's say we want to add a 95% confidence interval to our scatter plot using plt.fill_between. We need to calculate the standard error (SE) first, which is roughly equal to 1.96 * std(y) / mean(y).

Here's how you can do it:

import numpy as np
import matplotlib.pyplot as plt

# Scatter plot
x = [0.472202, ...] # your data here
y = [0.131113, ...]

(m, b) = np.polyfit(x, y, 1)
Y_Polyval = np.polyval([m, b], x)
plt.plot(x, Y_Polyval, linewidth=3, c="black")

CI = 1.96 * np.std(y) / np.mean(y)
plt.fill_between(y, (y-CI), (y+CI), color='blue', alpha=0.1)

# Add scatter plot
plt.scatter(x, y, s=250, linewidths=2, zorder=2)

plt.show()

Linear Model and Confidence Interval in ggplot2

ggplot2 is a popular R package for creating beautiful data visualizations. Here's how you can create a linear model with confidence intervals using ggplot2:

library(ggplot2)

# Linear model
lm_model <- lm(y ~ x, data = your_data)

# Confidence interval
ci <- confint(lm_model, level = 0.95)

# Plot
ggplot(data = your_data) +
 geom_point(aes(x = x, y = y)) +
 geom_line(aes(x = seq(min(x), max(x), by = 0.1),
 y = predict(lm_model, newdata = data.frame(x = seq(min(x), max(x), by = 0.1)))), color = "blue") +
 theme_classic()

These are just a few examples of how you can use confidence intervals in your scatter plot analysis. Remember to always consider the uncertainty involved in your estimation and take steps to ensure the accuracy of your results.