Dalam model regresi, memiliki nilai residual yang terdistribusi normal adalah kriteria penting untuk menghasilkan model yang akurat dan reliabel. Data yang berdistribusi normal seperti contoh jika dalam 100 buah jeruk semua rasa jeruk adalah asam, maka data tidak normal. Oleh karena itu, uji normalitas dilakukan untuk melihat apakah nilai residual terdistribusi normal atau tidak.
Model regresi memerlukan normalitas pada nilai residualnya, bukan pada masing-masing variabel penelitian. Uji normalitas dilakukan untuk menguji apakah variabel bebas/independent (X) dan variabel terikat/dependen (Y) dalam model regresi memiliki distribusi normal atau tidak (Juliandi et al., 2014).
Ajija (2011) menyarankan bahwa uji normalitas diperlukan ketika jumlah observasi kurang dari 30. Uji normalitas digunakan untuk mengetahui apakah error term mendekati distribusi normal. Jika jumlah observasi melebihi 30, maka tidak perlu dilakukan uji normalitas karena distribusi sampling error term telah mendekati normal. Jika misal menggunakan 285 observasi maka uji normalitas dapat diabaikan.
Namun, apabila data cenderung tidak normal maka dapat digunakan asumsi Central Limit Theorem, yaitu jika jumlah observasi lebih dari 30, maka tidak perlu dilakukan uji normalitas dan dapat diabaikan (Ajija et al., 2011:42).
Berikut ini adalah beberapa metode untuk melakukan uji normalitas:
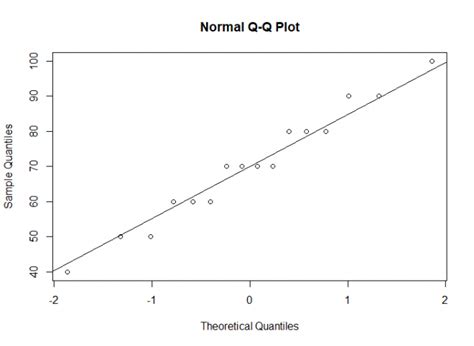
- Grafik histogram normal p-p plot: Distribusi yang normal akan membentuk suatu garis lurus diagonal. Jika distribusi data residual normal, maka garis yang menggambarkan data residual akan mengikuti garis diagonalnya.
- One Sample Kolmogorov-Smirnov: Kriteria pengambilan keputusan dari uji One Sample Kolmogorov-Smirnov adalah sebagai berikut: jika nilai signifikansi > 0,05 maka data yang digunakan dalam penelitian memiliki distribusi yang normal. Namun, kebalikannya, jika nilai signifikansi < 0,05 maka data yang digunakan tidak memiliki distribusi yang normal.
- Uji Shapiro-wilk: Kriteria pengambilan keputusan dari uji Shapiro-wilk adalah sebagai berikut: apabila nilai signifikansi > 0,05 , maka distribusi data memenuhi asumsi normalitas. Apabila nilai signifikansi < 0,05 , maka distribusi data tidak memenuhi asumsi normalitas.
Dengan demikian, uji normalitas adalah langkah penting dalam model regresi untuk mengetahui apakah residual terdistribusi normal atau tidak. Pemahaman yang baik tentang uji normalitas dapat membantu peneliti membuat keputusan yang tepat dalam analisis data dan menghasilkan model regresi yang akurat.
Referensi
Ajija, Shochrul Rohmatul, dkk. 2011. Cara Cerdas Menguasai Eviews. Jakarta: Salemba Empat.
Juliandi A, Irfan, Manurung S. 2014. Metodologi Penelitian Bisnis: Konsep dan Aplikasi. Medan: UMSU Press.
Sumber Gambar: Google Images