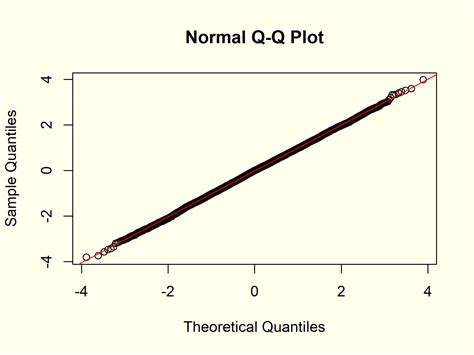
Dalam analisis statistik, keterkaitan (relationship) antara variabel-variabel menjadi penting. Salah satu metode untuk memahami keterkaitan ini adalah dengan menggunakan Q-Q plot. Dalam artikel ini, kita akan membahas penggunaan Q-Q plot untuk memeriksa apakah data berada pada distribusi normal atau tidak.

Skewed to the Right

Pertama, kita akan melihat contoh data yang terdistribusi ke kanan (skewed to the right). Dalam contoh ini, kita menggunakan distribusi eksponensial dengan parameter lambda = 3. Berikut adalah kode R untuk membuat Q-Q plot dan plot densitas:

par(mfrow = c(1, 2))
qqnorm(scale(x), pch = 16, cex = 1, col = "darkgray")
qqline(scale(x))

plot(density(scale(x)), 
 xlim = c(-3, 6), 
 ylim = c(0, 0.8), 
 lwd = 1.5, col = "red", 
 main = "Skewed to the right: X ~ exp(lambda = 3)")
z <- seq(-3, 6, by = 0.01)
lines(z, dnorm(z), lwd = 1.5, col = "black")
legend("topright", legend = c("Theoretical N(0, 1)", "Estimated density of the sample"), 
 lty = 1, lwd = 1.5, bty = "n", 
 col = c("black", "red"))

Skewed to the Left

Kemudian, kita akan melihat contoh data yang terdistribusi ke kiri (skewed to the left). Dalam contoh ini, kita menggunakan distribusi beta dengan parameter shape1 = 4 dan shape2 = 1. Berikut adalah kode R untuk membuat Q-Q plot dan plot densitas:

par(mfrow = c(1, 2))
qqnorm(scale(x), pch = 16, cex = 1, col = "darkgray")
qqline(scale(x))

plot(density(scale(x)), 
 xlim = c(-5, 4), 
 ylim = c(0, 0.6), 
 lwd = 1.5, col = "red", 
 main = "Skewed to the left: X ~ beta(4, 1)")
z <- seq(-4, 4, by = 0.01)
lines(z, dnorm(z), lwd = 1.5, col = "black")
legend("topright", legend = c("Theoretical N(0, 1)", "Estimated density of the sample"), 
 lty = 1, lwd = 1.5, bty = "n", 
 col = c("black", "red"))

Q-Q plot for Chi-Square Distribution

Selain itu, kita juga dapat menggunakan Q-Q plot untuk memeriksa distribusi chi-square. Berikut adalah kode R untuk membuat Q-Q plot:

set.seed(100)
y <- rchisq(500, df = 3)
x <- qchisq(ppoints(500), # 500 quantiles 생성
 df = 3)
qqplot(x, y, 
 main = expression("Q-Q plot for" ~~ {chi^2}[nu == 3]))
qqline(y, distribution = function(p) qchisq(p, df = 3), col = "red")

Application

Dalam aplikasinya, kita dapat menggunakan Q-Q plot untuk memeriksa distribusi data yang diperoleh dari suatu survei. Berikut adalah contoh penggunaan Q-Q plot dengan ggpubr package:

ggpubr::ggqqplot(x = "zvalue", 
 color = "Species", 
 facet.by = c("Species", "Measures"), 
 palette = c("#00AFBB", "#E7B800", "#FC4E07"), 
 ggtheme = ggpubr::theme_pubclean(base_size = 15)) 

Dalam kode di atas, kita menggunakan iris dataset untuk memeriksa distribusi z-score dari setiap variabel dan species. Q-Q plot ini dapat membantu kita dalam memahami keterkaitan antara variabel-variabel dan memeriksa apakah data berada pada distribusi normal atau tidak.

Dalam artikel ini, kita telah membahas penggunaan Q-Q plot untuk memeriksa distribusi data. Kita telah melihat contoh data yang terdistribusi ke kanan dan kiri, serta menggunakan distribusi chi-square sebagai contoh lain. Selain itu, kita juga telah membahas aplikasi Q-Q plot dengan ggpubr package. Dalam konklusi, Q-Q plot dapat menjadi salah satu alat yang berguna dalam memahami keterkaitan antara variabel-variabel dan memeriksa distribusi data.