Dalam analisis statistika, normalitas data adalah salah satu syarat penting sebelum melakukan pengujian hipotesis atau konstruksi interval kepercayaan. Namun, dalam beberapa kasus, data tidak memenuhi asumsi normalitas. Oleh karena itu, perlu dilakukan analisis lebih lanjut untuk mengetahui apakah data memiliki keterlambatan normalitas dan bagaimana cara mengatasi masalah tersebut.

Plot Kuantil-kuantil (QQ Plot)

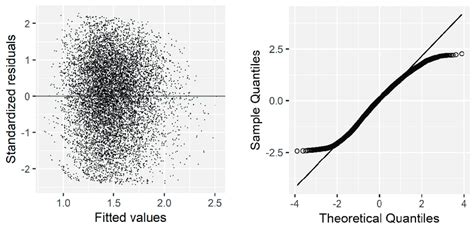
Plot kuantil-kuantil adalah salah satu alat analisis yang paling populer digunakan untuk menganalisis normalitas data. Dalam plot ini, pada sumbu-x terdapat kuantil teoritis dari distribusi normal standar, sedangkan pada sumbu-y terdapat fungsi distribusi empiris dari residu yang telah dikoreksi. Karena itu, apabila data memenuhi asumsi normalitas, maka titik-titik pada plot akan berada di garis lurus.

Dalam contoh yang diberikan, kita memiliki 50 titik yang harus dipetakan ke kuantil-kuantil standar normal. Berdasarkan fungsi kuantil standar normal, kita dapat mengetahui nilai x yang sesuai untuk titik-titik tersebut. Dengan demikian, plot ini memberikan informasi tentang bagaimana data seharusnya terdistribusi jika memenuhi asumsi normalitas.

Keterlambatan Normalitas

Dalam plot kuantil-kuantil di atas, kita dapat melihat bahwa beberapa titik berada di atas garis lurus. Hal ini menunjukkan bahwa data memiliki keterlambatan pada sisi kanan distribusi yang lebih besar daripada yang diperkirakan oleh distribusi normal standar. Karena itu, kita dapat menginterpretasikan bahwa data memiliki "ekor lebar" atau "fat tail" pada sisi kanan distribusi.

Pemeriksaan Lain

Ada beberapa cara lain untuk memeriksa keterlambatan normalitas. Salah satu cara adalah dengan menggunakan plot kepadatan (density plot) dan plot fungsi distribusi empiris (empirical CDF plot). Dalam density plot, kita dapat melihat bagaimana data terdistribusi dalam rentang nilai tertentu, sedangkan dalam empirical CDF plot, kita dapat melihat bagaimana data terdistribusi berdasarkan probabilitas.

Selain itu, kita juga dapat melakukan pemeriksaan normalitas dengan menggunakan uji Shapiro-Wilk. Dalam contoh yang diberikan, pemeriksaan ini menunjukkan bahwa p-value sebesar 0,02152, sehingga hipotesis nol (hipotesis bahwa data memenuhi asumsi normalitas) dapat ditolak.

Jika Ada Keterlambatan

Jika ada keterlambatan normalitas, kita perlu mengatasi masalah tersebut. Salah satu cara adalah dengan melakukan transformasi data. Contohnya, jika data memiliki simetri positif, maka transformasi logaritma dapat membantu menyelesaikan masalah tersebut.

Transformasi Data

Dalam contoh yang diberikan, kita melakukan transformasi logaritma terhadap variabel dependen dan kemudian menganalisis plot kuantil-kuantil, density plot, dan pemeriksaan normalitas lagi. Hasil analisis menunjukkan bahwa transformasi tersebut dapat membantu mengatasi keterlambatan normalitas.

Metode Lain

Ada beberapa metode lain yang dapat digunakan untuk mengatasi keterlambatan normalitas. Salah satu cara adalah dengan memiliki jumlah data yang cukup dan menggunakan teorema limit tengah (central limit theorem). Jika kita memiliki data yang cukup dan kita berharap bahwa varian errornya (anda dapat menggunakan residu sebagai proxy) adalah terbatas, maka kita dapat mengabaikan keterlambatan normalitas dan melakukan pengujian hipotesis atau konstruksi interval kepercayaan.

Metode lain adalah dengan menggunakan metode bootstrapping. Metode ini menggunakan resampling untuk mendapatkan statistik tentang data dan konstruksi interval kepercayaan.

Akhirnya, kita juga dapat menggunakan model linear umum (generalized linear models) yang menggeneralisasi regresi linier untuk kasus non-Gaussian error. Karena itu, jika kita berpikir bahwa respons masih berasal dari distribusi eksponensial, maka kita dapat menggunakan model ini untuk mengatasi keterlambatan normalitas.