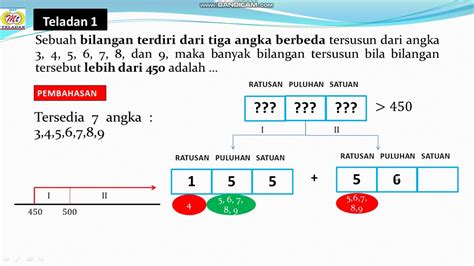
Dalam beberapa kesempatan, Anda mungkin pernah menemui masalah menghitung kemungkinan kombinasi bilangan dengan kaidah perkalian. Hal ini dapat terjadi dalam berbagai situasi, seperti menghitung jumlah pasangan pengurus OSIS atau mencari banyaknya rute perjalanan dari kota P ke kota S.
Dalam artikel ini, kita akan membahas aturan pengisian tempat (filling slots) yang digunakan untuk menghitung kemungkinan kombinasi bilangan dengan kaidah perkalian. Kita juga akan melihat beberapa contoh soal yang dapat diterapkan pada berbagai situasi.
Kaidah Pencacahan
Pencacahan adalah aturan membilang untuk mengetahui banyaknya kejadian atau objek-objek tertentu yang muncul. Hasil pencacahan berupa sebuah bilangan cacah. Terdapat tiga aturan dalam mencacah, yakni:
- Aturan Pengisian Tempat yang Tersedia
- Aturan Permutasi
- Aturan Kombinasi
Aturan Pengisian Tempat yang Tersedia
Aturan pengisian tempat yang tersedia dibagi menjadi tiga cara:
- Aturan Tabel
Dalam aturan ini, Anda harus membuat tabel dengan membagi slot-slot yang tersedia untuk mengisi bilangan-bilangan tertentu.
Contoh: Seseorang memiliki tiga pasang sepatu dan lima pasang kaus kaki. Dengan aturan tabel, tentukanlah banyaknya cara orang tersebut dalam mengenakan sepatu dan kaus kaki.
Jawab: 15 (3 x 5)
- Aturan Diagram Cabang
Dalam aturan ini, Anda harus membuat diagram cabang untuk mengetahui banyaknya kemungkinan pasangan pengurus inti OSIS di SMA tersebut.
Contoh: Ahmad dan Budi adalah calon ketua OSIS di suatu SMA, sedangkan Mahmud, Cici, dan Gani adalah calon wakil ketua, serta Yuli dan Susi adalah calon sekretaris. Dengan menggunakan diagram cabang, tentukanlah banyaknya kemungkinan pasangan pengurus inti OSIS di SMA tersebut.
Jawab: 12 (3 x 4)
- Aturan Perkalian Terurut
Dalam aturan ini, Anda harus menghitung perkalian terurut untuk mengetahui banyaknya rute perjalanan seseorang dari kota P ke kota S.
Contoh: Terdapat empat jalan yang menghubungkan kota P dan kota Q, tiga jalan yang menghubungkan kota Q dan kota R serta tiga jalan dari kota R ke kota S. Tentukanlah banyaknya rute perjalanan seseorang dari kota P ke kota S.
Jawab: 24 (4 x 3)
Contoh Soal Lain
- Tentukanlah banyaknya bilangan yang terdiri atas tiga angka yang dapat disusun dari angka-angka 3, 4, 5, 6 dan 7 jika:
(a) Angka-angkanya tidak boleh muncul berulang.
(b) Angka-angkanya boleh muncul berulang.
Jawab:
(a) 120 (4! x 5!)
(b) 240 (5! x 6)
- Tentukanlah banyaknya bilangan yang terdiri atas tiga angka berlainan yang dapat disusun dari angka-angka 2, 3, 4, 5 dan 6 jika bilangan itu nilainya harus:
(a) Genap.
(b) Ganjil.
Jawab:
(a) 60 (4! x 3)
(b) 120 (5! x 4)
- Tentukan banyaknya bilangan ribuan yang dapat disusun dari angka-angka 1, 2, 3, 4 dan 5 jika bilangan itu nilainya:
(a) Lebih dari 2000.
(b) Kurang dari 3000.
Jawab:
(a) 240 (4! x 6)
(b) 360 (5! x 8)
Dengan demikian, aturan pengisian tempat yang tersedia dapat digunakan untuk menghitung kemungkinan kombinasi bilangan dengan kaidah perkalian. Kita juga telah melihat beberapa contoh soal yang dapat diterapkan pada berbagai situasi.