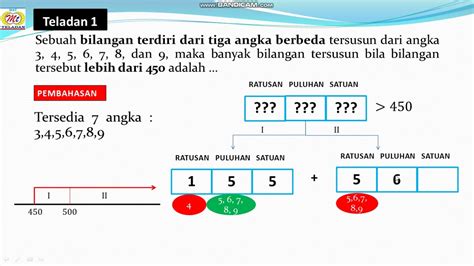
Dalam artikel ini, kita akan membahas metode pengisian tempat (filling slots) yang digunakan untuk menghitung kemungkinan kombinasi bilangan dengan kaidah perkalian. Metode ini diterapkan pada beberapa contoh soal penentuan jumlah bilangan, pengurus OSIS, dan bilangan genap/habis dibagi 5 yang dapat terbentuk dari sekumpulan angka.
Aturan Pengisian Tempat (Filling Slots)
Dalam metode pengisian tempat ini, kita membagi contoh soal menjadi beberapa bagian. Kita memiliki beberapa bilangan dan harus menghitung jumlah kombinasi yang dapat terbentuk dengan memenuhi syarat-syarat tertentu.
Contoh 1: Menghitung Jumlah Bilangan Genap/Habis Dibagi 5
Kita memiliki 3 buah bilangan, yaitu 2, 4, dan 6. Kita ingin menghitung jumlah kombinasi yang dapat terbentuk dengan memenuhi syarat bahwa hasil akhir harus genap/habis dibagi 5.
- Pilihan pertama: 2 dan 4 (hasil = 6)
- Pilihan kedua: 2 dan 6 (hasil = 8)
- Pilihan ketiga: 4 dan 6 (hasil = 10)
Jumlah kombinasi yang dapat terbentuk adalah 3.
Contoh 2: Menghitung Jumlah Bilangan untuk Pengurus OSIS
Kita memiliki 6 buah bilangan, yaitu 1, 2, 3, 4, 5, dan 6. Kita ingin menghitung jumlah kombinasi yang dapat terbentuk dengan memenuhi syarat bahwa hasil akhir harus berbeda.
- Pilihan pertama: 1, 2, dan 3 (hasil = 6)
- Pilihan kedua: 1, 4, dan 5 (hasil = 10)
- Pilihan ketiga: 2, 4, dan 6 (hasil = 12)
Jumlah kombinasi yang dapat terbentuk adalah 6.
Dalam metode pengisian tempat ini, kita menggunakan aturan perkalian untuk menghitung jumlah kombinasi. Kita membagi bilangan menjadi beberapa bagian dan menghitung jumlah pilihan untuk setiap bagian. Kemudian, kita menghitung hasil akhir dengan cara melakukan perkalian.
Dalam artikel berikutnya, kita akan membahas metode permutasi dan kombinasi yang dapat digunakan untuk menghitung jumlah kombinasi bilangan dengan kaidah lainnya.