Regresi linear adalah salah satu jenis analisis statistik yang digunakan untuk menentukan hubungan antara dua variabel. Dalam artikel ini, kita akan membahas tentang bentuk, arah, kuatnya, dan outliers dalam regresi linear.

Bentuk Regresi Linear

Regresi linear dapat memiliki berbagai bentuk, seperti linear, parabolic, atau lain-lain. Namun, dalam kasus sehari-hari, data seringkali menunjukkan hubungan yang linear, artinya bahwa perubahan variabel independen mengarah pada perubahan yang proporsional terhadap variabel dependen.

Arah Regresi Linear

Arah regresi linear dapat berupa positif atau negatif. Jika arahnya positif, maka perubahan variabel independen akan mengarah pada peningkatan variabel dependen. Sebaliknya, jika arahnya negatif, maka perubahan variabel independen akan mengarah pada penurunan variabel dependen.

Kuatnya Regresi Linear

Kuatnya regresi linear dapat diukur menggunakan koefisien korelasi (correlation coefficient) atau slope dari garis regresi. Koefisien korelasi yang tinggi menunjukkan adanya hubungan yang kuat antara dua variabel, sedangkan slope yang tinggi menunjukkan bahwa perubahan variabel independen akan mengarah pada perubahan yang lebih besar terhadap variabel dependen.

Outliers

Outliers adalah data point yang berada jauh dari garis trend. Jika data memiliki banyak outliers, maka kuatnya hubungan antara dua variabel akan menurun. Sebaliknya, jika data tidak memiliki outliers, maka hubungan antara dua variabel akan lebih kuat.

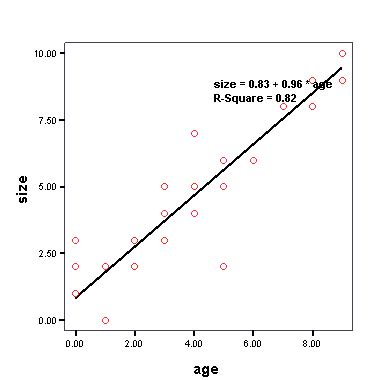
Contoh: Mari kita lihat contoh scatterplot yang menunjukkan hubungan linear:

Contoh 1

Dalam contoh ini, data point sangat terkonsentrasi dan tidak ada outliers. Maka, hubungan antara dua variabel adalah kuat dan linear.

Contoh 2

Dalam contoh ini, data point lebih tersebar dan memiliki beberapa outliers. Maka, hubungan antara dua variabel adalah moderat dan tidak linear.

Tujuan Regresi Linear

Tujuan regresi linear adalah untuk membuat prediksi terhadap nilai variabel dependen berdasarkan nilai variabel independen. Dengan cara ini, kita dapat mengetahui nilai yang tepat dari variabel dependen untuk suatu nilai variabel independen.

Dalam contoh di atas, jika kita ingin mengetahui nilai y untuk x = 9 atau x = 100, maka kita dapat menggunakan rumus regresi linear untuk membuat prediksi. Dengan cara ini, kita dapat memprediksi nilai y yang tepat berdasarkan nilai x.

Itulah analisis regresi linear yang dilakukan dalam statistika. Dalam bab berikutnya, kita akan membahas lebih lanjut tentang regresi non-linear dan bagaimana cara membuat prediksi terhadap data.