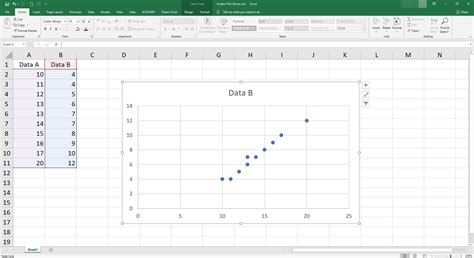
Garis Lurus dan Sumbu X-Y
Dalam membuat scatter diagram, kita perlu menggambar garis lurus horisontal untuk sumbu X dan garis lurus vertikal ke atas untuk sumbu Y. Dalam contoh ini, kita akan menggunakan data variabel independent (Masalah Painting) dan dependent (Tingkat Kekotoran). Berikut adalah langkah-langkah yang perlu dilakukan:
Garis Lurus Horisontal Sumbu X
Dengan menggunakan garis lurus horisontal, kita dapat menentukan skala untuk sumbu X. Skala ini akan membantu dalam memahami nilai variabel independent.
Garis Lurus Vertikal ke Atas Sumbu Y
Setelah membuat garis lurus horisontal, kita perlu menggambar garis lurus vertikal ke atas untuk sumbu Y. Dengan menggunakan garis lurus vertikal ini, kita dapat menentukan skala untuk sumbu Y.
Buat Titik-Titik Data
Selanjutnya, kita perlu membuat titik-titik data dengan cara mengambil sepasang data variabel independent dan dependent. Lalu, tarik lurus ke atas sampai pada lokasi nilai variabel dependent pada sumbu Y. Buat tanda titik koordinat pada lokasi kedua variabel tersebut bertemu, ulangi cara yang sama untuk semua data yang sudah dikumpulkan.
Lengkapi Informasi
Bubuhkan label yang diperlukan, contoh:
Judul diagram: Hubungan antara Masalah Painting dengan Tingkat Kekotoran
Judul sumbu X: Masalah Painting (K Unit)
Judul sumbu Y: Tingkat Kekotoran (K Unit)
Banyak data: n = 5
Periode: 1–10 Agustus 2011
Dibuat oleh: Eris
Cara Membaca Scatter Diagram
Ketika kita akan mengevaluasi scatter diagram, kita sebaiknya mempertimbangkan derajat korelasi beserta jenis-jenis korelasi yang sudah disimpulkan para ahli statistik seperti yang ditunjukkan pada Tabel 1 dan Tabel 2 di bawah ini.
Tabel 1. Derajat Korelasi
| Pola Scatter Diagram | Derajat Korelasi | Artinya |
|---|---|---|
| Tidak Ada | Tidak ada korelasi yang dapat dilihat. Variabel akibat (Y) tidak dipengaruhi oleh variabel penyebab (X) yang sedang dikaji. | |
| Lemah | Korelasi samar terlihat. Mungkin variabel penyebab (X) mempengaruhi variabel akibat (Y), tetapi tingkat pengaruhnya masih diragukan. Ada variabel X lain yang perlu dianalisis atau ada variasi signifikan di dalam variabel X tersebut. | |
| Kuat | Sebaran titik-titik mengelompok dalam bentuk linier yang jelas. Kemungkinan variabel penyebab (X) mempengaruhi langsung variabel akibat (Y). Oleh karena itu, setiap perubahan pada X akan memprediksi perubahan pada Y. | |
| Sempurna | Sebaran titik-titik jatuh pada sebuah garis lurus. Jika bentuknya seperti ini, dengan nilai variabel penyebab (X) tertentu kita dapat memprediksi secara pasti berapa nilai variabel akibat (Y). |
Tabel 2. Jenis-Jenis Korelasi
| Pola Scatter Diagram | Jenis Korelasi | Artinya |
|---|---|---|
| Positif | Peningkatan nilai variabel penyebab (X) menghasilkan peningkatan nilai variabel akibat (Y) | |
| Negatif | Peningkatan nilai variabel penyebab (X) menghasilkan penurunan nilai variabel akibat (Y) | |
| Nonlinier | Berbentuk kurva U atau S. Perubahan nilai variabel penyebab (X) menghasilkan perubahan nilai variabel akibat (Y) yang berbeda, tergantung posisi pada kurva. |
Dalam contoh scatter diagram di atas, derajat korelasi dan jenis korelasi belum secara jelas menunjukkan. Hal ini karena jumlah pasangan data sedikit (n=5). Oleh karena itu, para ahlinya statistik menyarankan pengumpulan data minimal n=30. Syarat-syarat tersebut penting dalam membuat scatter diagram yang akurat dan membantu dalam memahami hubungan antara variabel independen dan dependent.
Dengan demikian, membuat scatter diagram menjadi salah satu cara yang efektif dalam analisis korelasi dan memahami hubungan antara variabel independen dan dependent.