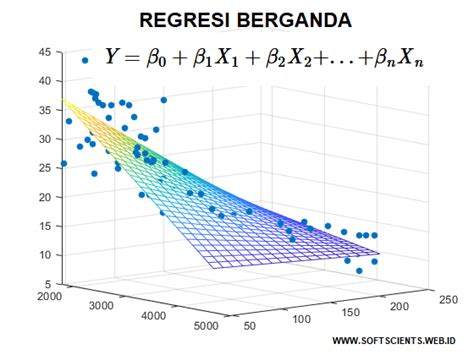
Dalam analisis statistik, regresi adalah salah satu metode yang paling umum digunakan untuk menjelaskan hubungan antara variabel-variabel. Dengan menggunakan SPSS (Statistical Product and Service Solution), kita dapat melakukan analisis regresi yang lebih efektif dan mudah dipahami.
Matriks Koefisien Korelasi
Matriks koefisien korelasi (Pearson Correlations) juga didapat dari pilihan Descriptive pada dialog box Statistics. Kita dapat melihat koefisien korelasi antar semua variabel. Pada matriks tersebut, didapatkan angka signifikansi untuk hubungan antar seluruh variabel independent dengan variabel dependent yang bernilai di bawah 0,05 (<0,05), sehingga dapat disimpulkan bahwa memang terdapat hubungan yang signifikan dan korelasi yang erat antara semua variabel independent dengan variabel dependent.
Variabel Entered/Removed
Hasil variabel Enter/Removed merupakan penentuan pilihan Enter (default) pada form Method, dialog box Option. Pada bagian ini, kita dapat memilih variabel-variabel yang akan digunakan dalam analisis regresi.
Model Summary
Pada bagian Model Summary, terdapat nilai koefisien determinasi R-Square = 0,932 (93,2%). Ini menunjukkan bahwa sebesar 93,2% variasi variabel dependent (Y) dapat dijelaskan oleh 2 variabel independent (X1 dan X2), artinya pengaruh variabel independen terhadap perubahan variabel dependen adalah 93,2%, sedangkan sisanya sebesar 6,8% dipengaruhi oleh variabel lain selain variabel independen X1 dan X2.
Anova
Pada bagian Anova, ditampilkan tabel analisis varian. Dari tabel di bawah didapat nilai F = 47,917 yang dapat digunakan untuk melakukan uji hipotesis atau F-test dalam memprediksi kontribusi variabel-variabel independent (X1 dan X2) terhadap variabel dependent (Y).
Hypothesis
H0: β1 = β2 = 0
H1: Minimal satu dari dua variabel tidak sama dengan nol
Dengan menentukan level of significant = 5% (0,05) dan degree of freedom untuk df1 = 2 dan df2 = 7, maka didapat dari tabel F-tabel = 4,74. Oleh karena F-hitung = 47,917 > F-tabel (0,05) = 4,74, maka H0 ditolak dan H1 diterima. Kesimpulannya, bahwa variabel independent (X1 dan X2) dengan signifikan memberikan kontribusi terhadap variabel dependent.
Coefficients
Pada bagian Coefficients, ditampilkan nilai koefisien regresi sehingga terbentuk persamaan regresi:
Ŷ = a + bX1 + cX2 = 16406,365 – 8,248X1 + 0,001X2
Pada bagian Unstandardized Coefficients ini ditampilkan juga Standard Error dari masing-masing variabel. Nilai pada kolom Beta, ditampilkan Z-score. Pada kolom berikutnya ditampilkan nilai t dari masing-masing variabel, yang dapat dimanfaatkan untuk menguji keberartian (t-Test) koefisien regresi yang didapatkan.
Residual Statistics
Pada bagian Residual Statistics, ditampilkan daftar hasil-hasil dari analisis residual statistics. Hasil ini digunakan untuk mengecek apakah residuals memiliki distribusi normal atau tidak.
Histogram
Pada bagian Histogram, ditampilkan histogram dari residuals. Dengan menggunakan histogram, kita dapat memeriksa apakah residuals memiliki distribusi normal atau tidak.
Normal Plot
Pada bagian Normal Plot, ditampilkan plot residu yang normal. Pada plot ini, kita dapat memeriksa apakah residuals memiliki distribusi normal atau tidak.
Scatter Plot
Pada bagian Scatter Plot, ditampilkan scatter plot dari variabel dependent dan independen. Dengan menggunakan scatter plot, kita dapat memeriksa hubungan antara variabel-variabel.
Analisis regresi sangat membantu untuk mendapatkan bukti ilmiah dari suatu hubungan antara variabel-variabel sekaligus meramalkannya. Dalam ilmu eksakta, hubungan antara variabel-variabel mudah dibuktikan karena memiliki prinsip-prinsip yang jelas dan konsisten. Namun, dalam ilmu sosial, hubungan antara variabel-variabel lebih kompleks dan memerlukan analisis yang lebih hati-hati.
Dalam artikel ini, kita telah mengetahui bagaimana SPSS digunakan untuk melakukan analisis regresi. Dengan menggunakan SPSS, kita dapat dengan mudah dan cepat melakukan analisis regresi dan menghasilkan laporan yang jelas dan akurat.