Dalam statistik, probabilitas dan fungsi kejadian adalah dua konsep yang terkait erat. Probabilitas bahwa x memiliki nilai kurang dari atau sama dengan X, didefinisikan sebagai:
P(X) = ∫∞−xp(x)dx
Sementara itu, fungsi kejadian density p(x) dapat dihubungkan dengan probabilitas P(X) melalui rumus diferensial:
p(x) = dP(X)/dX
Fungsi Kejadian untuk Variable Y
Jika variable y adalah fungsi monotonik dari x, yakni y = f(x), maka terdapat fungsi inversi x = g(y) dan dx/dy = dg(y)/dy. Fungsi kejadian density untuk y didefinisikan sebagai:
q(y) = p(g(y))|dg(y)/dy|
Di mana |dg(y)/dy| adalah nilai absolute dari turunan fungsi g(y) terhadap argumennya.
Contoh: Scattering Rutherford
Supposa bahwa partikel masuk berdistribusi seimbang di dalam beam dengan radius B, dan hanya ada satu inti target di tengah beam. Probabilitas bahwa parameter impak b adalah kurang dari atau sama dengan nilai b adalah luas lingkaran dengan jari-jari b sekitar inti target relatif terhadap luas beam πB²; yaitu:
P(b) = πb²/πB² = b²/B²
Sehingga fungsi kejadian density untuk b didefinisikan sebagai:
p(b) = 2b/B²
Rumus Scattering Rutherford
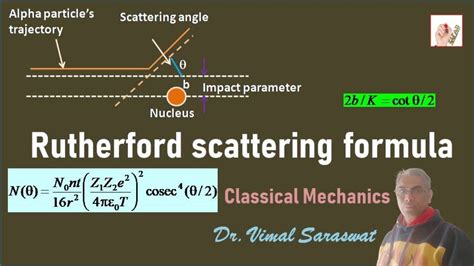
Hubungan antara parameter impak b dan sudut defleksi θ adalah:
b = γcos(θ/2)/sin(θ/2) = γcot(θ/2)
Dengan demikian, db/dθ = −γ/sin²(θ/2) dan |db/dθ| = γ/(2sin²(θ/2)).
Sebagai konsekuensi, probabilitas kejadian density untuk θ didefinisikan sebagai:
q(θ) = 2(γcot(θ/2)/B²;
yang dapat dipecah menjadi:
q(θ) = γ²[cos(θ/2)/sin³(θ/2)]/B²
Fomula Rutherford
Formula Rutherford adalah dalam bentuk kross-section untuk interaksi. Kross-section σ untuk parameter impak b adalah luas lingkaran dengan jari-jari b. Let Θ menjadi sudut defleksi yang sesuai dengan parameter impak b. Probabilitas bahwa parameter impak b kurang dari atau sama dengan nilai b adalah sama dengan probabilitas bahwa sudut defleksi akan lebih besar dari atau sama dengan Θ. Berdasarkan hubungan sebelumnya, maka:
σ(θ≥Θ) = πb² = πγ²cot²(Θ/2)
Generalisasi
Ada beberapa generalisasi yang menarik. Salah satunya memungkinkan untuk reaksi balik dari inti target sebagai hasil interaksi dengan partikel masuk. Generalisasi lainnya yang akan menarik adalah ketika gaya adalah dalam bentuk Aexp(−λr)/r².
Untuk informasi lebih lanjut tentang scattering dan difraksi partikel atom, lihat SCATTERING.