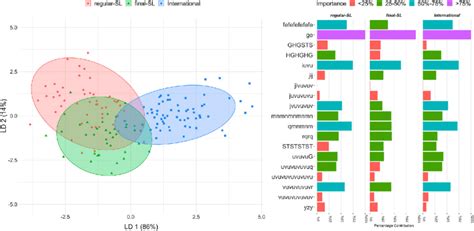
Diskriminan analysis (LDA) adalah sebuah teknik yang digunakan untuk menganalisis dan memprediksi kelas data berdasarkan nilai input. Dalam artikel ini, kita akan membandingkan analisis diskriminan (LDA) dengan logistic regression.

LDA vs Logistic Regression

Dalam model LDA, kita dapat menghitung log-odds sebagai berikut:

[  \text{log }\frac{Pr(G=k|X=x)}{Pr(G=K|X=x)}\
=  \text{log }\frac{\pi_k}{\pi_K}-\frac{1}{2}(\mu_k+\mu_K)^T\Sigma^{-1}(\mu_k-\mu_K) \
= a_{k0}+a_{k}^{T}x \ ]

Model LDA memenuhi asumsi model logistik linear.

Perbedaan antara model logistik linear dan LDA adalah bahwa model logistik hanya menjelaskan distribusi kondisional (Pr(G = k | X = x)). Tidak ada asumsi yang dibuat tentang (Pr(X)); sementara LDA menjelaskan distribusi bersamaan dari X dan G. (Pr(X)) adalah campuran Gaussian:

[Pr(X)=\sum_{k=1}^{K}\pi_k \phi (X; \mu_k, \Sigma) ]

where (\phi) adalah fungsi kepadatan Gaussian.

Selain itu, model logistik regression diselesaikan dengan mengoptimalkan likelihood kondisional G diberikan X: (Pr(G = k | X = x)); sementara LDA mengoptimalkan likelihood bersamaan dari G dan X: (Pr(X = x, G = k)).

Jika asumsi tambahan yang dibuat oleh LDA sesuai, maka LDA cenderung memperkirakan parameter lebih efisien dengan menggunakan informasi lebih banyak tentang data.

Kelebihan lainnya adalah bahwa sample tanpa label kelas dapat digunakan dalam model LDA. Sebaliknya, LDA tidak robust terhadap outliers kasus yang besar. Karena logistik regression bergantung pada asumsi yang lebih sedikit, maka tampaknya lebih robust terhadap tipe data non-Gaussian.

Contoh Simulasi

Dalam contoh di atas, kita memiliki input X yang adalah 1-D. Dua kelas memiliki prior yang sama dan kepadatan kelas-kelas densities X yang dipindahkan versi-satu sama lainnya, seperti ditampilkan dalam plot berikut ini:

Dalam setiap kepadatan kelas density X adalah campuran dua normal:

Kelas 1 (merah): 0.6N(-2, ¼ ) + 0.4N(0, 1).
Kelas 2 (biru): 0.6N(0, ¼ ) + 0.4N(2, 1).

Kepadatan kelas densities ditampilkan sebagai berikut:

Hasil LDA

Data pelatihan: 2000 sample untuk masing-masing kelas.

Data tes: 1000 sample untuk masing-masing kelas.

Mean dan variance dua kelas yang dipperkirakan oleh LDA adalah:

(\hat{\mu}_1) = -1.1948,
(\hat{\mu}_2) = 0.8224,
(\hat{\sigma}^2) = 1.5268.

Nilai batas antara dua kelas adalah ((\hat{\mu}_1 + \hat{\mu}_2) / 2 = -0.1862).

Error rate pada data tes adalah 0.2315.

Dengan distribusi yang benar, nilai batas optimal adalah -0.7750 dan error rate adalah 0.1765. 

Kepadatan kelas dalam LDA ditampilkan sebagai berikut. Kedua kepadatan kelas adalah Gaussian dan dipindahkan versi-satu sama lainnya, seperti asumsi oleh LDA.

Hasil Logistic Regression

Logistic regression linear mendapatkan:

(\beta = (-0.3288, -1.3275)^T).

Nilai batas memenuhi (-0.3288 – 1.3275X = 0), maka setara dengan -0.2477.

Error rate pada data tes adalah 0.2205.

Kepadatan posterior yang dipperkirakan adalah:

[ Pr(G=1|X=x) =\frac{e^{- 0.3288-1.3275x}}{1+e^{- 0.3288-1.3275x}} \ ]

Kesimpulan

Dalam artikel ini, kita membandingkan analisis diskriminan (LDA) dengan logistic regression. Kita melihat bahwa LDA memiliki kelebihan dan kekurangan tersendiri. Dalam beberapa kasus, LDA dapat lebih efisien dalam mengoptimalkan likelihood bersamaan dari G dan X. Namun, LDA tidak robust terhadap outliers kasus yang besar dan memerlukan asumsi tambahan yang sesuai.