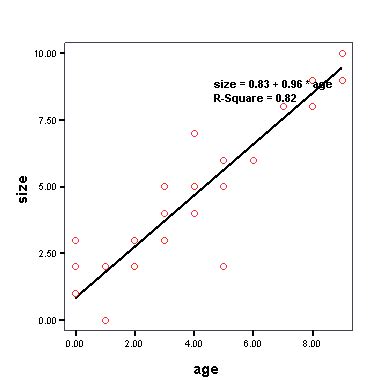
Dalam statistika, keterkaitan linier (linear relationship) adalah suatu hubungan antara dua variabel yang memiliki bentuk linier. Dalam artikel ini, kita akan membahas bagaimana keterkaitan linier dan outliers mempengaruhi data.
Keterkaitan Linier Kuat
Keterkaitan linier kuat terjadi ketika semua data point sangat terkonsolidasi dan tidak ada outlier yang signifikan. Dalam kasus ini, data menunjukkan keterkaitan linier kuat. Contohnya adalah scatterplot berikut:
+---------------+
| Data Point |
+---------------+
| * |
| *** |
| ******** |
| *********** |
+---------------+
Keterkaitan Linier Sedang
Keterkaitan linier sedang terjadi ketika data point tidak sangat terkonsolidasi dan memiliki beberapa atau banyak outlier. Dalam kasus ini, data menunjukkan keterkaitan linier sedang. Contohnya adalah scatterplot berikut:
+---------------+
| Data Point |
+---------------+
| * |
| *** |
| ********** |
| *********** |
| ****************|
+---------------+
Outliers
Outlier adalah data point yang berada jauh dari garis trend. Dalam kasus keterkaitan linier, outliers dapat mempengaruhi data dan membuatnya tidak linier. Contohnya adalah scatterplot berikut:
+---------------+
| Data Point |
+---------------+
| * |
| *** |
| ********** |
| *********** |
| ****************|
| O |
+---------------+
Dalam kasus ini, data point "O" adalah outlier yang berada jauh dari garis trend. Dengan menghilangkan beberapa atau banyak outliers, kita dapat meningkatkan keterkaitan linier antara dua variabel.
Tujuan Regresi
Tujuan regresi adalah untuk mencari sebuah persamaan yang dapat digunakan untuk membuat prediksi. Dalam contoh di atas, kita memiliki data berikut:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| … | … |
Dengan menggunakan regresi linier, kita dapat mencari sebuah persamaan yang dapat digunakan untuk membuat prediksi. Contohnya adalah persamaan berikut:
y = 0,5x + 3
Persamaan ini dapat digunakan untuk membuat prediksi nilai y jika kita memiliki nilai x. Misalnya, jika kita ingin mengetahui nilai y saat x = 9, maka kita dapat menghitungnya sebagai berikut:
y = 0,5(9) + 3
= 4,5
Dengan demikian, tujuan regresi adalah untuk mencari sebuah persamaan yang dapat digunakan untuk membuat prediksi.