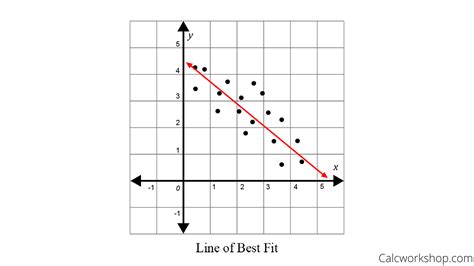
Dalam analisis regresi linier, line of best fit (LOBF) berperan penting sebagai garis lurus yang mampu menjelaskan persebaran data. Selain itu, LOBF juga berfungsi untuk memperlihatkan kecenderungan tren. Namun, bagaimana kita dapat mengetahui apakah garis tersebut sesuai dengan persebaran data?

Untuk menjawab pertanyaan tersebut, kita perlu memahami dua hal: garis itu sendiri dan residual. Garis yang menggambarkan korelasi data disebut LOBF, sedangkan residual adalah jarak antara setiap titik data yang tersebar dengan garis.

Kita dapat mengetahui apakah garis tersebut sesuai dengan persebaran data dengan cara menghitung SUM dari residual yang dipangkatkan. Semakin dekat hasil dengan angka 0, semakin sesuai garis tersebut.

Least Square: Mencari Kemiringan Garis yang Tepat

Untuk menemukan garis yang tepat, kita dapat menggunakan least square dengan rumus y = a + bX. y adalah variabel dependen, a adalah konstanta atau intercept, b adalah kemiringan garis, dan X adalah variabel independen.

Dalam R, kita dapat menggunakan fungsi linear model dengan lm(). Berikut contoh penggunaannya:

regresi <- lm(formula = Kecepatan.Lari ~ Berat.Badan, data=data)
regresi

[1]
Call:
lm(formula = Kecepatan.Lari ~ Berat.Badan, data = data)

Coefficients:
(Intercept) Berat.Badan 
 -1.8116 0.2342

Mari fokus pada intercept dan kecepatan lari. Intercept atau konstanta adalah a, sementara angka 0.2342 merepresentasikan b. Maka dapat disimpulkan bahwa Kecepatan Lari = -1.8116 + 0.2342 * Berat Badan.

Visualisasi Garis dengan Abline

Sekarang, saatnya buat visualisasi garis berdasarkan hasil linear model yang telah kita terapkan. Gunakan fungsi abline() dan isi parameter dengan fungsi linear model untuk membuat garis:

plot(data, xlab="Berat Badan", ylab="Kecepatan Lari")
abline(regresi)

Mengenal Scatterplot

Scatterplot adalah visualisasi persebaran titik-titik data yang setiap titiknya berada di koefisien variabel x dan y. Garis tengah dalam visualisasi regresi merepresentasikan line of best fit, yaitu garis yang menjelaskan tren dari persebaran data.

Pola Korelasi

Pola korelasi dapat dibedakan menjadi beberapa bentuk:

• Positive Correlation: Y cenderung meningkat mengikuti penambahan nilai x.
• Negative Correlation: Nilai x yang rendah malah berada di y yang tinggi.
• No Correlation: Nilai y dan x membentuk persebaran titik secara acak.

Kesimpulan

Line of best fit (LOBF) adalah garis lurus yang mampu menjelaskan persebaran data. Kita dapat mengetahui apakah garis tersebut sesuai dengan persebaran data dengan cara menghitung SUM dari residual yang dipangkatkan. Selain itu, kita juga dapat menggunakan least square untuk mencari kemiringan garis yang tepat dan visualisasinya dengan abline().