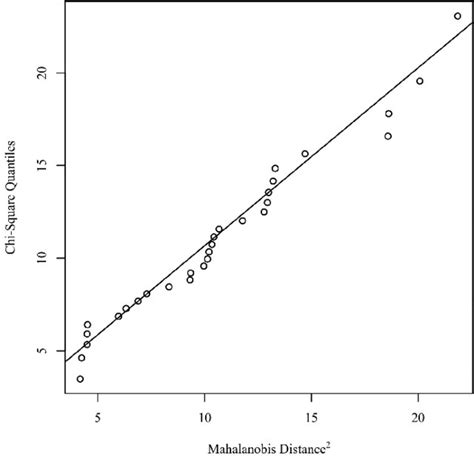
Dalam statistika, chi-square adalah suatu metode yang digunakan untuk menghitung probabilitas bahwa data berada di luar wilayah prediksi tertentu. Dalam kasus ini, kita memiliki empat variabel dan perlu menggunakan chi-square dengan empat derajat kebebasan.
Untuk mendapatkan elips prediksi dengan tingkat kepercayaan 95%, kita menghitung nilai chi-square dengan empat derajat kebebasan, yaitu 9.49. Kita lalu menggantikan nilai terbesar eigenvalue, yakni 26.245, dengan hasil perkalian 9.49 dan akhirnya mencari akar kvadrat dari hasil tersebut. Dalam hal ini, kita mendapatkan elips prediksi dengan panjang setengahnya sebesar 15.782, seperti di bawah ini:
$$ l_1 = \sqrt{\lambda_1\chi^2_{4,0.05}} $$
$$ = \sqrt{26.245 \times 9.49} $$
$$ = 15.782 $$
Sementara itu, arah dari sumbu pertama dapat dilihat dari eigenvektor pertama. Dalam hal ini, kita melihat bahwa nilai yang besar berada pada variabel Informasi, Kemiripan, dan Arithmetik. Hal ini menunjukkan bahwa sumbu tersebut berarah kearah peningkatan nilai pada variabel-variabel tersebut.
Panjang setengah sumbu kedua dapat dihitung dengan menggantikan nilai eigenvalue kedua sebesar 6.255, lalu melakukan perkalian dengan 9.49 dan mencari akar kvadrat dari hasil tersebut. Dalam hal ini, kita mendapatkan panjang setengah sumbu sebesar 7.705 atau kurang lebih separuh panjang sumbu pertama.
$$ l_2 = \sqrt{\lambda_2\chi^2_{4,0.05}} $$
$$ = \sqrt{6.255 \times 9.49} $$
$$ = 7.705 $$
Dalam gambaran yang lebih rinci, kita dapat melihat bahwa sumbu kedua memiliki panjang setengahnya sebesar 7.705, kurang lebih separuh panjang sumbu pertama.
Kita juga dapat melakukan perhitungan yang sama untuk sumbu ketiga, seperti di bawah ini:
$$ l_3 = \sqrt{\lambda_1\chi^2_{4,0.05}} $$
$$ = \sqrt{3.931 \times 9.49} $$
$$ = 6.108 $$
Sumbu ketiga memiliki panjang setengahnya sebesar 6.108, yang tidak jauh berbeda dengan panjang sumbu kedua. Sumbu ini berarah kearah peningkatan nilai pada variabel Gambaran Kompleksi dan Informasi, serta penurunan nilai pada Kemiripan dan Arithmetik.
Sedangkan sumbu terpendek memiliki panjang setengahnya sebesar 4.260 seperti di bawah ini:
$$ l_4 = \sqrt{\lambda_4\chi^2_{4,0.05}} $$
$$ = \sqrt{1.912 \times 9.49} $$
$$ = 4.260 $$
Sumbu ini berarah kearah peningkatan nilai pada Kemiripan dan Gambaran Kompleksi, serta penurunan nilai pada Informasi.
Bentuk overall dari elips dapat dihitung dengan mengkomparasikan panjang sumbu-sumbu tersebut. Dalam hal ini, kita memiliki bentuk yang mirip dengan bola sepak sedikit memanjang.
Kita juga dapat mencari volume dari hyper-elips menggunakan rumus yang diberikan sebelumnya. Kembali, nilai kritis dari chi-square jika kita ingin mendapatkan elips prediksi dengan tingkat kepercayaan 95%, dengan empat derajat kebebasan adalah 9.49. Dalam hal ini, kita menggantikan nilai eigenvalue dengan hasil perkalian 9.49 dan mencari akar kvadrat dari hasil tersebut. Volume hyper-elips dapat dihitung sebagai berikut:
$$ \frac{2\pi^{p/2}}{p\Gamma\left(\frac{p}{2}\right)}(\chi^2_{p,\alpha})^{p/2}|\Sigma|^{1/2} $$
$$ = \frac{2\pi^2}{4\Gamma(2)}(9.49)^2|(0, 0, 0, 0)|^{1/2} $$
$$ \approx 15.782 $$
Dalam penutup, kita dapat melihat bahwa metode chi-square sangat berguna dalam menghitung bentuk elips prediksi dengan tingkat kepercayaan tertentu. Dengan demikian, perlu dipertimbangkan dalam analisis statistika yang lebih lanjut.