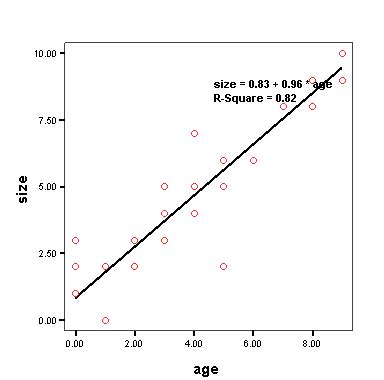
Sebagai alat statistik yang sangat sederhana, scatter diagram digunakan untuk menunjukkan hubungan antara dua variabel. Diagram ini sering digabungkan dengan garis regresi linear sederhana untuk membangun model antara dua variabel. Untuk menjelaskan hal ini, saya mengumpulkan data dari perjalanan saya ke La Brea Tar Pits, sebuah formasi alam yang terletak di Los Angeles.
La Brea Tar Pits adalah formasi alamiah yang telah ada selama ribuan tahun, membentuk trap alami yang kontributif pada kematian awal banyak hewan tidak beruntung yang terserang oleh lumpur. Sejak 1940-an, lubang-lubang ini telah digali, menghasilkan penemuan banyak fosil, termasuk Mammoths, Wolf, Bear, serta beberapa hewan lainnya seperti Singa Amerika dan Domba Amerika.
Mayoritas aktivitas dan ekspedisi saat ini berpusat di Pit 91. Pada perjalanan saya ke La Brea, ilmuwan dan peneliti aktif bekerja di Pit 91. Berikut adalah foto Pit 91 serta data yang saya pilih untuk memperkenalkan scatter plot.
Dalam gambar tersebut, jumlah spesimen yang ditemukan setiap tahun ditunjukkan. Hasilnya dalam bentuk tabel adalah sebagai berikut:
| Tahun | # Spesimen |
|---|---|
| 2004 | 2,452 |
| 2005 | 3,826 |
| 2006 | 1,189 |
| 2007 | 3,388 |
Dengan cara sederhana, scatter plot menempatkan titik di mana setiap tahun bertemu dengan jumlah spesimen yang dikumpulkan pada tahun itu.
Fitur lain dari scatter plots adalah kemudahan penyelesaian menggunakan regresi linear sederhana. Dalam Microsoft Excel, ini dapat dilakukan dengan memasukkan garis trendline. Hasilnya adalah plot berikut ini:
Banyak orang yang menanyakan bagaimana garis ini dihitung dan apa artinya. Garis ini adalah model yang berasal dari regresi linear sederhana data. Dasar garis ini adalah persamaan yang kita semua pelajari di sekolah, yaitu y = mx + b, di mana y adalah jumlah spesimen dan x adalah tahun. Dalam kasus khusus ini, persamaan untuk garisnya adalah y = 217,1x – 432680 atau # Spesimen = 217,1*tahun – 432680.
Penghitungan garis ini sedikit lebih kompleks. Nilai m dan b (slope dan intercept) dihitung dari data menggunakan regresi linear sederhana.
Persamaan ini memastikan jarak setiap titik ke garis adalah minimal. Grafiknya dapat dilihat di plot berikut ini.
Jarak setiap titik ke garis adalah kesalahan, yang ditunjukkan dalam gambar sebagai e1, e2, e3, dan e4. Garis regresi linear mengembalikan nilai m (slope) dan b (intercept) yang mengurangi jumlah kesalahan kuadrat. Dapat dikatakan bahwa m dan b dihitung untuk meminimalisir (e12 + e22 + e32 + e42).
Sederetan lain untuk regresi linear sederhana adalah "regresi persegi terkecil", nama yang menggambarkan hasil alat tersebut.
Sementara itu, mungkin dapat dipasang garis melalui data mana pun, namun tidak berarti Anda harus. Jika tidak ada hubungan antara tahun dan jumlah spesimen, maka kita tidak seharus-menggunakan model yang menunjukkan bahwa ada hubungan. Salah satu statistik komplementer dengan regresi adalah nilai p (p-value), kadang-kadang disebut p(2-Tail).
Hasil output dari SPC XL berikutnya memiliki statistik regresi termasuk nilai p untuk variabel Tahun.
Kita dapat yakin (1-p Value)*100% bahwa perubahan pada tahun menyebabkan perubahan pada jumlah spesimen yang ditemukan. Nilai p untuk tahun adalah 0,461, yang berarti kita dapat yakin (1-0,461)*100% atau 54% bahwa perubahan pada tahun menyebabkan perubahan pada jumlah spesimen yang ditemukan.
Pada tingkat kepercayaan 54%, kita biasanya tidak akan mengambil kesimpulan bahwa perubahan pada variabel tahun menyebabkan perubahan pada jumlah spesimen yang ditemukan.
Diagram scatter dengan model regresi adalah alat yang sangat baik untuk menunjukkan hubungan antara dua variabel. Dalam contoh ini, diagram membantu memahami hubungan antara jumlah spesimen dan tahun.
Namun, perlu diingat bahwa diagram hanya menggambarkan relasi statistik dan tidak berarti ada hubungan kausal (hubungan sebab-akibat) antara dua variabel.