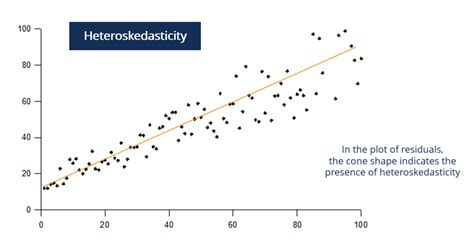
Dalam analisis regresi, heteroskedastisitas adalah masalah yang dapat muncul ketika variancia residual tidak konstan. Dalam artikel ini, saya akan membahas tiga metode untuk menyelesaikan masalah ini: meredefinisi variabel, regresi berat, dan transformasi variable dependen.
Meredefinisi Variabel
Jika model Anda adalah model sektoral yang memiliki perbedaan besar antara ukuran observasi, Anda dapat mencari cara lain untuk spesifikasi model yang mengurangi dampak perbedaan ukuran. Cara ini dilakukan dengan mengubah model dari menggunakan nilai asli menjadi menggunakan nilai rate dan nilai kapita. Tentu saja, model seperti itu akan menjawab pertanyaan yang sedikit berbeda. Anda harus menentukan apakah pendekatan ini sesuai untuk data Anda dan apa yang Anda ingin pelajari.
Saya lebih suka metode ini karena tidak melibatkan manipulasi data asli sebanyak yang lain. Hanya variabel-variabel yang perlu diubah dalam cara yang seringkali logis. Dengan demikian, Anda harus berpikir tentang cara lain untuk spesifikasi model, yang kerap menghasilkan model yang lebih baik daripada hanya menghilangkan heteroskedastisitas.
Dalam contoh data kita, kami menggunakan populasi untuk memprediksi jumlah kecelakaan. Jika Anda berpikir tentang itu, tidaklah mengherankan bahwa kota-kota dengan populasi besar memiliki lebih banyak kecelakaan. Namun, kami dapat mengubah model sehingga kami menggunakan populasi untuk memprediksi tingkat kecelakaan. Pendekatan ini diskon dampak skala dan mendapatkan kepada perilaku yang terkini.
Regresi Berat
Regresi berat adalah metode yang menugaskan setiap titik data dengan berat berdasarkan variancia nilai fitnya. Ide-nya adalah memberikan berat kecil pada observasi yang terkait dengan variancia yang lebih tinggi untuk mengurangi residu kuadrat. Regresi berat mengoptimalkan sum dari residu kuadrat yang diweight. Ketika Anda menggunakan berat yang benar, heteroskedastisitas digantikan oleh homoskedastisitas.
Saya lebih suka pendekatan ini kurang karena regresi berat melibatkan manipulasi data yang lebih banyak dan kurang intuitif. Namun, jika Anda dapat mengidentifikasi variabel yang terkait dengan perubahan variancia, pendekatan umum adalah menggunakan invers dari variable tersebut sebagai berat. Dalam kasus kita, kolom Weight dalam dataset sama dengan 1 / Populasi.
Kembali ke model asli kami, saya akan menggunakan Accidents sebagai variabel dependen dan Population sebagai variabel independen. Namun, saya akan meminta software untuk melakukan regresi berat dan menerapkan kolom berat. Gambar residu di bawah ini menunjukkan bahwa regresi berat telah memperbaiki heteroskedastisitas.
Transformasi Variable Dependen
Saya selalu simpan transformasi data sebagai pilihan terakhir karena melibatkan manipulasi data yang paling banyak dan membuat hasil interpretatif sulit. Ide-nya adalah Anda mengubah data asli menjadi nilai lain yang menghasilkan residu yang baik. Jika tidak ada yang lain bekerja, coba transformasi untuk menghasilkan homoskedastisitas.
Saya akan merefit model asli kami namun menggunakan transformasi Box-Cox pada variabel dependen.
Seperti Anda lihat, transformasi data tidak menghasilkan homoskedastisitas dalam dataset ini. Itu baik karena saya tidak ingin menggunakan pendekatan ini! Kami akan tetap dengan model regresi berat.
Perlu diingat bahwa ada banyak alasan untuk heteroskedastisitas. Identifikasi penyebab dan menyelesaikan masalah untuk menghasilkan homoskedastisitas dapat memerlukan pengetahuan subjek yang luas. Dalam kebanyakan kasus, tindakan remedial untuk heteroskedastisitas yang serius diperlukan. Namun, jika tujuan utama Anda adalah memprediksi jumlah total variabel dependen daripada mengestimasi efek khusus variabel independen, Anda mungkin tidak perlu memperbaiki variancia non-konstan.
Jika Anda belajar regresi dan menyukai pendekatan yang saya gunakan di blog saya, coba baca artikel tentang "Analisis Regresi untuk Pemula" yang dapat membantu Anda memahami konsep dasar analisis regresi.