Kurva standar normal adalah kurva yang paling umum digunakan dalam statistik dan matematika. Kurva ini memiliki rata-rata 0 dan deviasi standar 1. Dalam artikel ini, kita akan membahas tentang bagaimana cara menggambarkan kurva standar normal dengan menggunakan kuartil.

Kuartil

Kuartil adalah salah satu konsep yang paling penting dalam statistik. Kuartil adalah nilai yang menunjukkan 25% atau 75% data berada di atasnya. Dalam kurva standar normal, kuartil 0.5 (50%) adalah 0. Nilai ini menunjukkan bahwa separuh data berada di atas 0 dan separuh lainnya berada di bawah 0.

Menggambarkan Kurva Standar Normal dengan Kuartil

Rumus untuk menggambarkan kurva standar normal adalah sebagai berikut:

• Kuartil 0.01: -2,26
• Kuartil 0.95: 1,64

Kita dapat menggunakan fungsi qnorm dalam R untuk mendapatkan kuartil dari kurva standar normal.

qnorm(seq(0.01,0.99,0.01))

Menggambarkan Data dengan Kuartil

Selain itu, kita juga dapat menggambarkan data dengan menggunakan fungsi quantile dalam R. Contohnya, kita dapat menggambarkan 200 data random dari kurva standar normal dan kemudian mencari kuartil untuk nilai 0.01 hingga 0.99.

quantile(rnorm(200), probs = seq(0.01,0.99,0.01))

Menggambarkan QQ Plot

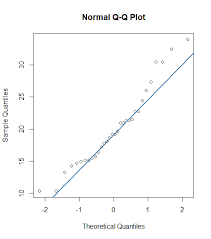
QQ plot adalah grafik yang menunjukkan data sample terhadap kuartil teoretis dari distribusi teoritis. Dalam R, kita dapat menggunakan fungsi qqnorm dan qqplot untuk menggambarkan QQ plot.

Contoh Menggunakan Fungsi qqnorm

Kita dapat menggunakan fungsi qqnorm untuk menggambarkan data sample terhadap kuartil teoretis dari kurva standar normal. Contohnya, kita dapat menggambarkan data Height dari dataset trees yang datang dengan R.

qqnorm(trees$Height)

Contoh Menggunakan Fungsi qqplot

Fungsi qqplot dapat digunakan untuk menggambarkan QQ plot untuk distribusi apapun. Contohnya, kita dapat menggunakan fungsi qqplot untuk menggambarkan data random dari distribusi uniform (0,1) terhadap kuartil teoretis dari distribusi uniform yang sama.

y <- qunif(ppoints(length(randu$x)))
qqplot(randu$x, y)

Menginterpretasikan Hasil

Jika point-point dalam QQ plot jatuh pada garis lurus, maka data sample dapat dianggap berasal dari distribusi teoritis yang digunakan. Jika point-point tidak jatuh pada garis lurus, maka data sample mungkin tidak sesuai dengan distribusi teoritis yang digunakan.

Contoh Menggunakan Fungsi qqplot untuk Distribusi Skewed

Kita dapat menggunakan fungsi qqplot untuk menggambarkan data sample terhadap kuartil teoretis dari distribusi chi-square (3 derajat kebebasan) untuk mendapatkan QQ plot yang menunjukkan bahwa data sample tidak sesuai dengan distribusi normal.

qqplot(qnorm(ppoints(30)), qchisq(ppoints(30), df=3))

Contoh Menggunakan Fungsi qqplot untuk Distribusi dengan "Heavy Tails"

Kita dapat menggunakan fungsi qqplot untuk menggambarkan data sample terhadap kuartil teoretis dari distribusi Cauchy untuk mendapatkan QQ plot yang menunjukkan bahwa data sample memiliki nilai ekstrem lebih banyak daripada yang diharapkan jika datanya berasal dari distribusi normal.

qqplot(qnorm(ppoints(30)), qcauchy(ppoints(30)))

Dalam kesimpulan, kuartil adalah salah satu konsep yang penting dalam statistik dan dapat digunakan untuk menggambarkan kurva standar normal. Fungsi qnorm dan quantile dalam R dapat digunakan untuk mencari kuartil dari kurva standar normal. Selain itu, fungsi qqnorm dan qqplot juga dapat digunakan untuk menggambarkan QQ plot yang menunjukkan apakah data sample sesuai dengan distribusi teoritis yang digunakan.