Dalam statistik dan data science, plot-probabilitas (probability plot) adalah sebuah teknologi yang sangat berguna untuk memvisualisasikan distribusi kumulatif suatu variable. Dalam artikel ini, kita akan membahas tentang plot-probabilitas PP, yaitu plot-probabilitas yang menampilkan fungsi densitas kumulatif.
Plot-probabilitas QQ (quantile-quantile) lebih umum digunakan dalam praktek, karena memiliki deviasi lebih tinggi di ujung (2 tails). Sebaliknya, plot-probabilitas PP memiliki deviasi yang lebih tinggi di tengah. Karena itu, researchers sering memberikan perhatian lebih pada ujung, sehingga plot-probabilitas QQ lebih populer dalam praktek.
Untuk membuat plot-probabilitas PP, kita dapat menggunakan fungsi probplot dari scipy.stats atau qqplot dari statsmodel, karena mereka menghasilkan hasil yang serupa.
Anatomy of a Normal Probability Plot
Plot-probabilitas normal adalah alat yang sangat berguna untuk tes asumsi normalitas. Ia lebih akurat daripada histogram, yang tidak dapat mendeteksi deviasi-subtil, dan tidak mengalami masalah dengan power yang terlalu banyak atau terlalu sedikit, seperti pada tes normalitas.
Ada dua versi plot-probabilitas normal: Q-Q dan P-P. Saya akan mulai dengan Q-Q. Plot-probabilitas Q-Q menampilkan setiap nilai observasi melawan distribusi normal standar dengan jumlah titik yang sama. Kita memiliki 111 pengamatan dalam data set ini, dan Anda dapat melihat histogram distribusi pada kanan, serta plot-probabilitas Q-Q di kiri.
Di bawahnya terlihat adalah nilai-nilai observasi, disusun dari rendah ke tinggi. Anda dapat melihat bahwa nilai-nilai berjalan dari sekitar -2.2 hingga 2.2. (Catatan: Nilai-nilai ini telah diasumsikan sebelum digambar, sehingga mereka sudah memiliki rata-rata 0 dan deviasi standar 1. Jika tidak, plot akan menstandardisasi nilainya sebelum digambar).
Pada sumbu Y terlihat adalah nilai-nilai yang Anda dapatkan jika mereka datang dari distribusi normal standar dengan jumlah titik yang sama—111.
Konsep ini mungkin sedikit aneh jika Anda belum familiar dengan itu, maka pikirkan sebentar. Ingat kembali ke kelas statistika intro Anda, ketika Anda belajar aturan tentang distribusi normal standar:
Rata-rata adalah 0 dan deviasi standar adalah 1
34% titik berada di bawah rata-rata dan satu deviasi standar
12,5% titik berada di antara satu dan dua deviasi standar di bawah rata-rata
2,5% titik berada di atas dua deviasi standar di bawah rata-rata
Karena distribusi ini simetris, persentase-persentase yang sama juga berlaku di atas rata-rata.
Dalam distribusi 111 titik dengan rata-rata 0 dan deviasi standar 1, kita tahu bahwa titik ke-56 harus memiliki nilai 0—dalam distribusi normal mediannya sama dengan rata-ratanya.
Hanya 2,5% dari 111 titik—sekitar 3 titik—yang seharusnya memiliki nilai di bawah -2. Maka nilai ketiga seharusnya berada di sekitar -2.
Demikian pula, terdapat nilai yang sesuai untuk titik ke-17, ke-42, dan seterusnya. Kita tidak memiliki cara mudah untuk mengingat mereka, tapi nilai-nilai tersebut digambar pada grafik.
Jika setiap nilai tepat di mana seharusnya, jika distribusi sempurna normal, maka setiap titik akan jatuh tepat di garis. Semakin jauh titik dari garis, semakin jauh ia dari tempat yang dianggap normal oleh distribusi.
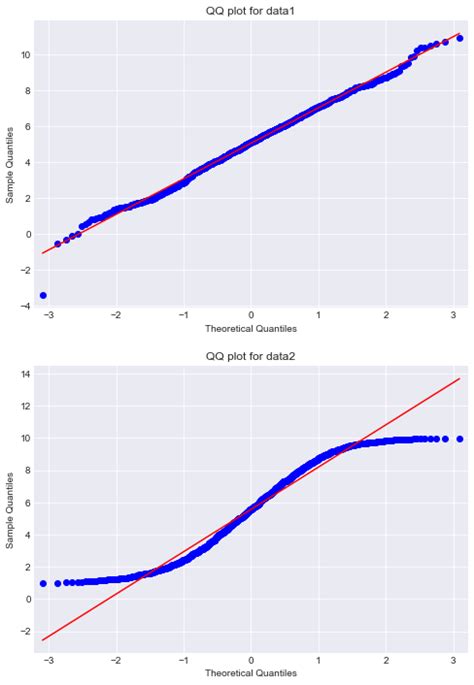
Plot-probabilitas Q-Q berikut menunjukkan distribusi yang berskew ke kanan. Anda dapat melihat bahwa tidak seimbang dengan distribusi normal sama sekali—terlalu banyak nilai rendah dan terlalu sedikit nilai tinggi.
Saya menemukan bantu membaca plot-probabilitas Q-Q dengan melihat histogram di sampingnya, untuk memperjelas hasil.