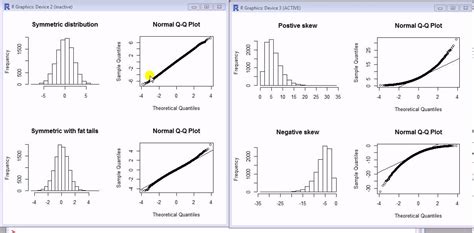
Dalam analisis statistik, kurva bell (juga dikenal sebagai distribusi normal standard) adalah distribusi yang sangat penting. Kurva ini memiliki mean 0 dan deviasi standar 1. Pada titik 0,5 atau kuartil ke-50, nilai probabilitasnya adalah 0. Lebih dari setengah data berada di bawah 0, yaitu puncak hump dalam kurva.
Kuartil 0,95 atau 95%ile memiliki nilai sekitar 1,64. Sebagian besar data berada di bawah 1,64. Berikut adalah kode R yang menghasilkan kuartil untuk distribusi normal standar dari 0,01 hingga 0,99 denganincrement 0,01:
qnorm(seq(0.01,0.99,0.01))
Kita juga dapat secara acak mengenerate data dari distribusi normal standar dan kemudian menemukan kuartilnya. Di sini, kita generate contoh sebesar 200 dan menemukan kuartil untuk 0,01 hingga 0,99 menggunakan fungsi quantile:
quantile(rnorm(200), probs = seq(0.01,0.99,0.01))
Jadi kita lihat bahwa kuartil adalah secara efektif data Anda disusun dalam urutan ascending, dengan berbagai data point yang terlabel sebagai titik di bawah mana 1% atau 5% data jatuh. Namun, perlu dicatat bahwa ada banyak cara untuk menghitung kuartil. Fungsi quantile() di R menawarkan 9 algoritma kuartil yang berbeda! Lihat help(quantile) untuk informasi lebih lanjut.
Plot Kuadrat (QQ plot) memplotkan data Anda, disusun dalam urutan ascending, dan kemudian memplotkan versus kuartil yang dihitung dari distribusi teoretis. Banyaknya kuartil dipilih untuk cocok dengan ukuran data Anda. Sementara plot normal QQ adalah yang paling umum digunakan dalam praktek karena banyak metode statistik mengasumsikan normalitas, plot Kuadrat dapat dibuat untuk distribusi apapun.
Di R, ada dua fungsi untuk membuat plot Kuadrat: qqnorm() dan qqplot().
Fungsi qqnorm() membuat plot Kuadrat normal. Anda memberi vektor data, dan R memplotkan data dalam urutan ascending versus kuartil dari distribusi normal standar. Contoh, pertimbangkan data trees yang datang dengan R. Data ini memberikan pengukuran tinggi, girth, dan volume kayu di 31 pohon cherry hitam. Salah satu variabelnya adalah Height. Dapat kita asumsi bahwa sampel tinggi-tingginya berasal dari populasi yang tersebar normal?
Itu tampak seperti asumsi yang relatif aman. Titik-titik tampak jatuh di atas garis lurus. Perhatikan sumbu-x memplotkan kuartil teoritis. Itu adalah kuartil-kuartil dari distribusi normal standar dengan mean 0 dan deviasi standar 1.
Fungsi qqplot() memungkinkan Anda membuat plot Kuadrat untuk distribusi apapun. Berbeda dengan fungsi qqnorm(), Anda harus memberikan dua argumen: data pertama dan data kedua. Mari lihat data randu yang datang dengan R. Data ini adalah frame data yang mengandungi 3 kolom bilangan acak di interval (0,1). Bilangan acak harus tersebar normal. Oleh karena itu kita dapat memeriksa asumsi ini dengan membuat plot Kuadrat terhadap data acak disusun dalam urutan ascending versus kuartil dari distribusi teoritis uniform (0,1).
Di sini, kita membuat plot Kuadrat untuk kolom pertama bilangan, yang disebut x:
y <- qunif(ppoints(length(randu$x)))
qqplot(randu$x,y)
Fungsi ppoints() menghasilkan jumlah probabilities atau proportions yang diinginkan. Saya ingin nilai-nilai yang sama dengan randu$x, jadi saya berikan argumen length(randu$x), yang mengembalikan 400. Fungsi qunif() lalu menghasilkan 400 kuartil dari distribusi uniform untuk 400 proporsi. Saya simpan itu ke y dan kemudian memplot y versus randu$x menggunakan fungsi qqplot.
Apabila data Anda tidak sesuai dengan asumsi normalitas, maka perlu dilakukan uji normalitas terlebih dahulu sebelum membuat plot Kuadrat.