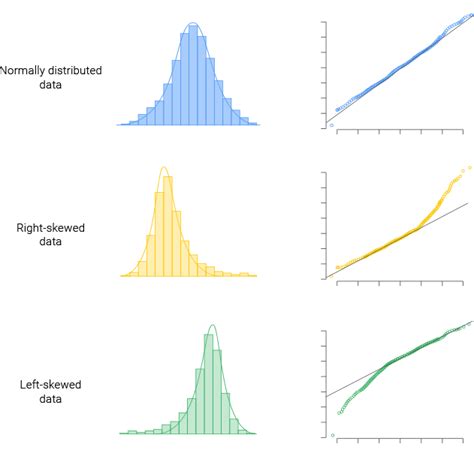
Dalam analisis statistik, data yang simetris memainkan peranan penting dalam menentukan metode analisis apa yang sesuai. Data yang simetris memiliki grafik seperti kurva distribusi normal, yaitu berbentuk seperti lonceng, setangkup, seimbang di sisi kiri dan kanan. Sehingga sebelum dilakukan analisis lebih lanjut, kita harus mengetahui kesimetrisan dari data tersebut.
Ada beberapa cara untuk mengidentifikasi apakah data simetris atau berdistribusi normal, antara lain melalui diagram batang dan daun atau melalui diagram kotak. Namun, salah satu alat grafis yang paling efektif dalam menguji kesimetrisan data adalah Q-Q Plot (Quantile-Quantile Plot).
Q-Q Plot adalah plot kuantil-kuantil yang membantu kita untuk menguji apakah suatu set data berasal dari beberapa distribusi teoritis seperti berdistribusi normal atau tidak. Kuantil memberikan informasi mengenai posisi data karena kuantil membagi data menjadi bagian-bagian yang sama.
Dalam Q-Q Plot, kuantil data empiris dan kuantil distribusi teoritis tersebut berasal dari distribusi yang sama, maka grafik yang diperoleh akan membentuk garis lurus. Misalnya, Q-Q plot yang dibuat adalah diagram pencar antara kuantil data yang diurutkan terhadap kuantil normal standar yang berkorespondensi dengannya membentuk garis lurus maka data yang dimiliki berdistribusi normal.
Namun, perlu diingat bahwa Q-Q Plot tidak akan memberikan informasi yang berguna jika ukuran sampel yang kita gunakan terlalu kecil, sehingga diharapkan sampel yang digunakan berukuran n≥20.
Untuk menentukan kelinieran dari Q-Q Plot, kita dapat menghitung koefisien korelasi titik-titik dalam plot tersebut. Koefisien korelasi ini dinamakan koefisien korelasi antara kuantil data terurut dengan kuantil normal standar, yaitu:
rQ = (Σ(xj – x̄)(qj – q̄)) / (√(Σ(xj – x̄)^2) √(Σ(qj – q̄)^2))
rQ adalah koefisien korelasi yang menunjukkan terdapat hubungan yang kuat antara x dengan q karena x dan q memiliki distribusi yang sama. Sebagai dasar dalam menyimpulkan, nilai rQ dibandingkan dengan rtabel, jika rQ > rtabel maka data berdistribusi normal pada tingkat signifikansi α.
Berikut ini adalah tabel nilai tabel untuk pemeriksaan koefisien korelasi:
| r | 0.05 |
|---|---|
| 0.35 | 1.96 |
| 0.50 | 1.48 |
| 0.75 | 1.15 |
Dalam artikel ini, kita telah membahas tentang pemeriksaan kesimetrisan data dan Q-Q Plot. Kita juga telah mengetahui cara untuk menghitung koefisien korelasi titik-titik dalam plot tersebut. Sebagai bahan tambahan, berikut adalah beberapa artikel menarik kami tentang Kesimetrisan Data:
- Kesimetrisan Data: Pengertian dan Pentingnya
- Menguji Kesimetrisan Data dengan Q-Q Plot
- Analisis Statistik untuk Data yang Simetris
Tonton juga video pilihan dari kami berikut ini:
- Q-Q Plot: Cara Membuat dan Menginterpretasikan
- Menguji Kesimetrisan Data dengan Diagram Batang dan Daun
Silakan baca juga beberapa artikel menarik kami tentang Kesimetrisan Data, daftar lengkapnya adalah sebagai berikut:
- Kesimetrisan Data: Pengertian dan Pentingnya
- Menguji Kesimetrisan Data dengan Q-Q Plot
- Analisis Statistik untuk Data yang Simetris
Saya harap artikel ini telah memberikan Anda informasi yang berguna tentang pemeriksaan kesimetrisan data dan Q-Q Plot. Jika Anda memiliki pertanyaan atau ingin mengetahui lebih lanjut, silakan hubungi kami di [email protected].