Dalam analisis regresi linear, normalisasi dan linieritas merupakan dua asumsi penting yang harus dipenuhi untuk mendapatkan hasil yang akurat. Asumsi ini memungkinkan kita untuk mengetahui apakah data kita terdistribusi secara normal dan homoskedastik.

Pemeriksaan Sisaan

Pada dasarnya, pemeriksaan sisaan dilakukan dengan menggunakan plot dan diagram, seperti P-P plot, histogram, Q-Q plot, stem-leaf plot, dan boxplot. Plot ini membantu kita mengetahui apakah data kita terdistribusi secara normal dan homoskedastik.

P-P plot (Probability-Probability plot) digunakan untuk membandingkan distribusi probabilitas dari data dengan distribusi probabilitas normal. Plot ini membantu kita mengetahui apakah data kita terdistribusi secara normal atau tidak.

Histogram digunakan untuk memvisualisasikan distribusi frekuensi dari data. Histogram membantu kita mengetahui apakah data kita terdistribusi secara simetrik atau tidak, serta apakah ada outliers (nilai yang sangat jauh dari nilai lainnya).

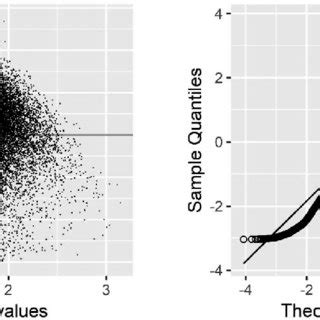
Q-Q plot (Quantile-Quantile plot) digunakan untuk membandingkan distribusi kuartil dari data dengan distribusi kuartil normal. Plot ini membantu kita mengetahui apakah data kita terdistribusi secara normal atau tidak.

Stem-leaf plot dan boxplot digunakan untuk memvisualisasikan distribusi data dan mencari outliers.

Pemeriksaan Homoskedastisitas

Pada dasarnya, pemeriksaan homoskedastisitas dilakukan dengan menggunakan residual plot. Plot ini membantu kita mengetahui apakah data kita terdistribusi secara homoskedastik atau tidak.

Residual plot menampilkan nilai sisa (residual) versus nilai prediksi. Plot ini membantu kita mengetahui apakah data kita terdistribusi secara homoskedastik, yaitu apakah nilai sisa sama dalam semua nilai prediksi.

** Kesimpulan**

Dalam analisis regresi linear, normalisasi dan linieritas merupakan dua asumsi penting yang harus dipenuhi untuk mendapatkan hasil yang akurat. Pemeriksaan sisaan dan pemeriksaan homoskedastisitas dapat membantu kita mengetahui apakah data kita terdistribusi secara normal dan homoskedastik atau tidak. Dengan demikian, kita dapat membuat keputusan yang lebih baik dalam analisis regresi linear.